题目内容
若复数z满足z•i=1-i，则z= ．
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：由条件利用两个复数相除，分子和分母同时乘以分母的共轭复数，计算求得结果．
解答：
解：∵z•i=1-i，
∴z=
=
=-1-i，
故答案为：-1-i．
∴z=
| 1-i |
| i |
| -i(1-i) |
| -i2 |
故答案为：-1-i．
点评：本题主要考查两个复数代数形式的乘除法，虚数单位i的幂运算性质，属于基础题．
练习册系列答案
相关题目
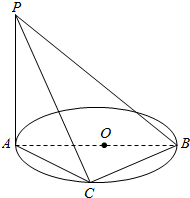如图，AB是圆O的直径，AB=5，PA垂直于圆O所在的平面，C是圆周上一点，AC=PA=4，求：
如图，在△ABC中，AB=AC，过点A的直线与△ABC的外接圆交于点P，交BC的延长线于点D，用数学归纳法证明
+
+…+
≥
，从n=k到n=k+l，不等式左边需添加的项是（ ）
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 3n |
| 5 |
| 6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|