题目内容
设函数f（x）的图象关于直线x=1对称，当x≤1时，f（x）=x2+1，当x＞1时，求函数f（x）的解析式．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：由题意可得f（x）=f（2-x），可得x＞1时，2-x≤1，代入已知解析式化简可得．
解答：
解：∵函数f（x）图象关于直线x=1对称，∴f（x）=f（2-x）
∵当x≤1，f（x）=x2+1
∴x＞1时，2-x≤1，
∴f（x）=f（2-x）=（2-x）2+1=x2-4x+5，
∴当x＞1时，求函数f（x）的解析式为：f（x）=x2-4x+5
∵当x≤1，f（x）=x2+1
∴x＞1时，2-x≤1，
∴f（x）=f（2-x）=（2-x）2+1=x2-4x+5，
∴当x＞1时，求函数f（x）的解析式为：f（x）=x2-4x+5
点评：本题考查函数解析式的求解，利用对称性得出f（x）=f（2-x）是解决问题的关键，属基础题．
练习册系列答案
相关题目
函数f（x）=（2x-3）ex的单调递增区间是（ ）
A、（-∞，
| ||
| B、（2，+∞） | ||
C、（0，
| ||
D、（
|
如图，已知ABCD是空间四边形，AB=AD，CB=CD，求证：BD⊥AC．
已知四棱锥P-ABCD的底面为菱形，且∠ABC=60°，AB=PC=2，AP=BP=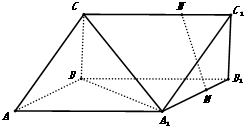
如图，三棱柱中ABC-A1B1C1，CA=CB，AB=AA1，∠BAA1=60°，点M和N分别为线段A1B1和CC1上的点，且A1M=2MB1，MN∥平面A1BC．求证：
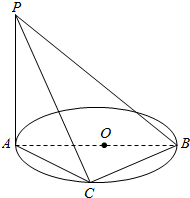如图，AB是圆O的直径，AB=5，PA垂直于圆O所在的平面，C是圆周上一点，AC=PA=4，求：