题目内容
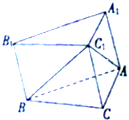如图，在斜三棱柱ABC-A1B1C1的底面△ABC中，∠BAC=90°，且BC1⊥AC，过C1作C1H⊥底面ABC，垂足为H，则点H在（ ）| A、直线AC上 |
| B、直线AB上 |
| C、直线BC上 |
| D、△ABC内部 |
考点：直线与平面垂直的判定
专题：空间位置关系与距离
分析：由条件，根据线面垂直的判定定理，AC⊥平面ABC1，又AC在平面ABC内，根据面面垂直的判定定理，平面ABC⊥平面ABC1，
则根据面面垂直的性质，在平面ABC1内一点C1向平面ABC作垂线，垂足必落在交线AB上．
则根据面面垂直的性质，在平面ABC1内一点C1向平面ABC作垂线，垂足必落在交线AB上．
解答：
解：如图：
∵∠BAC=90°，∴AC⊥AB，
∵BC1⊥AC，∴AC⊥BC1，
而BC1、AB为平面ABC1的两条相交直线，根据线面垂直的判定定理，AC⊥平面ABC1，
又AC在平面ABC内，根据面面垂直的判定定理，平面ABC⊥平面ABC1，
则根据面面垂直的性质，在平面ABC1内一点C1向平面ABC作垂线，垂足必落在交线AB上．
故选：B
解：如图：∵∠BAC=90°，∴AC⊥AB，
∵BC1⊥AC，∴AC⊥BC1，
而BC1、AB为平面ABC1的两条相交直线，根据线面垂直的判定定理，AC⊥平面ABC1，
又AC在平面ABC内，根据面面垂直的判定定理，平面ABC⊥平面ABC1，
则根据面面垂直的性质，在平面ABC1内一点C1向平面ABC作垂线，垂足必落在交线AB上．
故选：B
点评：本题主要考查空间中线面垂直、面面垂直的判定定理与性质定理，属于中档题．
练习册系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
函数y=
log2x2的定义域是（ ）
| 1 |
| 2 |
| A、R |
| B、（0，+∞） |
| C、{x∈R|x≠0} |
| D、[0，+∞） |
已知集合A={x|-2≤x≤1}，B={y|y=2x+3，x∈A}，C={y|y=x2，x∈A}，求B∩C=（ ）
| A、[0，4] |
| B、[-1，5] |
| C、[1，4] |
| D、[-1，4] |
已知集合P={y|y=-x2+2，x∈R}，Q={y|y=x，x∈R}，则P∩Q=（ ）
| A、R |
| B、{y|y≤2} |
| C、{y|y≥2} |
| D、{y|y＞2} |
已知半圆x2+y2=3（y≥0），P为半圆上任一点，A（2，0）为定点，以PA为边作正三角形PAB，（如图所示）求四边形POAB面积的最大值．