题目内容
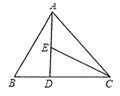如图所示，在△ABC中，| BD |
| 1 |
| 2 |
| DC |
| AE |
| ED |
| AB |
| a |
| AC |
| b |
| CE |
考点：平面向量的基本定理及其意义
专题：计算题,平面向量及应用
分析：由
=
，得到
=
+
，由于
=3
，则
=3（
-
），则有
=
=
+
，再由
=
-
即可得到．
| BD |
| 1 |
| 2 |
| DC |
| AD |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
| AE |
| ED |
| AE |
| AD |
| AE |
| AE |
| 3 |
| 4 |
| AD |
| 1 |
| 2 |
| a |
| 1 |
| 4 |
| b |
| CE |
| AE |
| AC |
解答：
解：若
=
，
=
，
=
，
则
-
=
（
-
），
则有
=
+
=
+
，
则
=
-
=
-
，
由于
=3
，
则
=3（
-
），
则有
=
=
+
，
故
=
-
=
-
．
故答案为：
-
．
| AB |
| a |
| AC |
| b |
| BD |
| 1 |
| 2 |
| DC |
则
| AD |
| AB |
| 1 |
| 2 |
| AC |
| AD |
则有
| AD |
| 2 |
| 3 |
| AB |
| 1 |
| 3 |
| AC |
| 2 |
| 3 |
| a |
| 1 |
| 3 |
| b |
则
| CD |
| AD |
| AC |
| 2 |
| 3 |
| a |
| 2 |
| 3 |
| b |
由于
| AE |
| ED |
则
| AE |
| AD |
| AE |
则有
| AE |
| 3 |
| 4 |
| AD |
| 1 |
| 2 |
| a |
| 1 |
| 4 |
| b |
故
| CE |
| AE |
| AC |
| 1 |
| 2 |
| a |
| 3 |
| 4 |
| b |
故答案为：
| 1 |
| 2 |
| a |
| 3 |
| 4 |
| b |
点评：本题考查平面向量基本定理及运用，考查向量的运算，属于中档题．
练习册系列答案
相关题目
已知集合A={x|-2≤x≤1}，B={y|y=2x+3，x∈A}，C={y|y=x2，x∈A}，求B∩C=（ ）
| A、[0，4] |
| B、[-1，5] |
| C、[1，4] |
| D、[-1，4] |
已知半圆x2+y2=3（y≥0），P为半圆上任一点，A（2，0）为定点，以PA为边作正三角形PAB，（如图所示）求四边形POAB面积的最大值．函数f（x）满足f（x）•f（x+2）=13，若f（1）=2，则f（99）=（ ）
| A、13 | ||
| B、2 | ||
C、
| ||
D、
|