湖面上漂着一球.湖结冰后将球取出.冰面上留下了一个直径为24cm.深为8cm的空穴.则该球的体积为$\frac{8788}{3}π$cm3．题目和参考答案——青夏教育精英家教网—

题目内容

20．湖面上漂着一球，湖结冰后将球取出，冰面上留下了一个直径为24cm，深为8cm的空穴，则该球的体积为$\frac{8788}{3}π$cm³．

分析先设出球的半径，进而根据球的半径，球面上的弦构成的直角三角形，根据勾股定理建立等式，求得r，最后根据球的表面积公式求得球的体积．

解答解：设球的半径为r，依题意可知12²+（r-8）²=r²，解得r=13．
∴球的体积为$\frac{4}{3}$πr³=$\frac{8788}{3}π$cm³．
故答案为：$\frac{8788}{3}π$cm³．

点评本题主要考查了球面上的勾股定理和球的面积公式．属基础题．

练习册系列答案

11．

2014年某大学自主招生面试环节中，七位评委为一考生打出分数的茎叶图如图21，去掉一个最高分和一个最低分，所剩数据的平均数，众数和中位数分别为（　　）

8．设函数f（x）的定义域为D，如果存在正实数k，使对任意x∈D，都有x+k∈D，且f（x+k）＞f（x）恒成立，则称函数f（x）为D上的“k型增函数”．已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=|x-a|-2a，若f（x）为R上的“2 015型增函数”，则实数a的取值范围是（　　）

A．

（-∞，$\frac{2015}{4}$）

B．

（$\frac{2015}{4}$，+∞）

C．

（-∞，$\frac{2015}{6}$）

D．

（$\frac{2015}{6}$，+∞）

15．直线$|\begin{array}{l}{x}&{y}\\{2}&{1}\end{array}|$=3的一个方向向量可以是（-2，-1）．．

5．如果关于x的不等式|x-2|+|x+3|≥a的解集为R，求参数a的取值范围．

12．一个几何体的三视图如图所示，则该几何体的体积为（　　）

9．

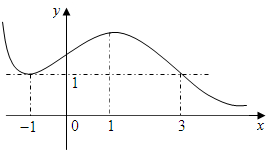f′（x）为定义在R上的函数f（x）的导函数，而y=3^f'（x）的图象如图所示，则y=f（x）的单调递增区间是（-∞，3]．

10．平面上到定点A（-1，3）距离为1且到定点B（3，6）距离为d的直线共有2条，则d的取值范围是（　　）

试题分类