题目内容
8.定义在R上的函数f(x)满足:f(x)=$\frac{1}{2}$f(x-2π),且当x∈[0,2π)时,f(x)=8sinx,则函数g(x)=f(x)-lgx的零点个数是( )| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
分析 求出函数的解析式,利用函数的图象以及函数值判断即可.
解答 解:定义在R上的函数f(x)满足:f(x)=$\frac{1}{2}$f(x-2π),且当x∈[0,2π)时,f(x)=8sinx,
当x∈[2π,4π)时,f(x)=4sinx,
当x∈[4π,6π)时,f(x)=2sinx,
当x∈[6π,8π)时,f(x)=sinx,
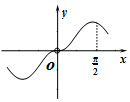
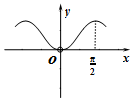
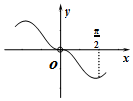
在坐标系中画出两个函数y=f(x)与y=lgx的图象如图:
由图象可知两图象有5个交点,故函数g(x)=f(x)-lgx有5个零点,
故选A.
点评 本题考查了函数零点与函数图象的关系,属于中档题.

练习册系列答案
相关题目
16.已知函数f(x)=$\frac{{{{({x+1})}^2}+ln({\sqrt{1+9{x^2}}-3x})cosx}}{{{x^2}+1}}$,且f(2017)=2016,则f(-2017)=( )
| A. | -2014 | B. | -2015 | C. | -2016 | D. | -2017 |
3.已知圆${C_1}:{(x+6)^2}+{(y-5)^2}=4$,圆${C_2}:{(x-2)^2}+{(y-1)^2}=1,M,N$分别为圆C1和C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )
| A. | 7 | B. | 8 | C. | 10 | D. | 13 |
13.已知函数$f(x)=\left\{\begin{array}{l}xlnx-3x,x>0\\{x^2}+\frac{3}{2}x,x≤0\end{array}\right.$的图象上有且只有四个不同的点关于直线y=-1的对称点在直线y=kx-1上,则实数k的取值范围是( )
| A. | $({\frac{2}{7},1})$ | B. | $({\frac{1}{3},3})$ | C. | $({\frac{1}{2},2})$ | D. | $({2,\frac{7}{2}})$ |
20.已知函数f(x)=-2x5-x3-7x+2,若f(a2)+f(a-2)>4,则实数a的取值范围( )
| A. | (-∞,1) | B. | (-∞,3) | C. | (-1,2) | D. | (-2,1) |
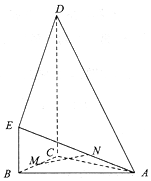 如图,多面体ABCDE中,AB=AC,平面BCDE⊥平面ABC,BE∥CD,CD⊥BC,BE=1,BC=2,CD=3,M为BC的中点.
如图,多面体ABCDE中,AB=AC,平面BCDE⊥平面ABC,BE∥CD,CD⊥BC,BE=1,BC=2,CD=3,M为BC的中点.