题目内容
3.已知圆${C_1}:{(x+6)^2}+{(y-5)^2}=4$,圆${C_2}:{(x-2)^2}+{(y-1)^2}=1,M,N$分别为圆C1和C2上的动点,P为x轴上的动点,则|PM|+|PN|的最小值为( )| A. | 7 | B. | 8 | C. | 10 | D. | 13 |
分析 求出圆C1关于x轴的对称圆的圆心坐标A,以及半径,然后求解圆A与圆C2的圆心距减去两个圆的半径和,即可求出|PM|+|PN|的最小值.
解答 解:圆C1关于x轴的对称圆的圆心坐标A(-6,-5),半径为2,圆C2的圆心坐标(2,1),半径为1,
|PM|+|PN|的最小值为圆A与圆C2的圆心距减去两个圆的半径和,
即:$\sqrt{(-6-2)^{2}+(-5-1)^{2}}$-3=7.
故选:A.
点评 本题考查圆的对称圆的方程的求法,考查两个圆的位置关系,两点距离公式的应用,考查转化思想与计算能力,考查数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
11.若集合A={x|x-x2>0},B={x|(x+1)(m-x)>0},则“m>1”是“A∩B≠∅”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.已知实数x,y满足$\left\{\begin{array}{l}{x-y≥-3}\\{2x+y≤3}\\{y≥1}\end{array}\right.$,则z=x+2y的最大值为( )
| A. | 0 | B. | 3 | C. | 6 | D. | 7 |
18.某学校食堂推出两款优惠套餐,甲、乙、丙三位同学选择同一款餐的概率为( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
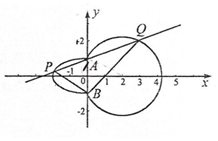 如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.
如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.