题目内容

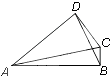如图，在四边形ABCD中，AB⊥BC，AD⊥DC．若
AB
=
a
，
AD
=
.
b
，则
AC
•
BD
=（　　）
A、
a
2-
b
2
B、
b
2-
a
2
C、
a
2+
b
2
D、
a
•
b
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：由BC⊥AB，可得
AC
•
AB
=（
AB
+
BC
）•
AB
=
a
2．同理可得：
AC
•
AD
=
b
2．由于
BD
=
AD
-
AB
，代入
AC
•
BD
，整理可得．
解答： 解：∵BC⊥AB，
∴
AC
•
AB
=（
AB
+
BC
）•
AB
=
a
2．
同理可得：
AC
•
AD
=
b
2．
∵
BD
=
AD
-
AB
，
∴
AC
•
BD
=
AC
•(
AD
-
AB
)=
AC
•
AD
-
AC
•
AB
=
a
2-
b
2．
故选A．
点评：本题考查了向量的加减法的运算以及向量垂直的数量积性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
已知数列﹛an﹜的前n项和Sn=
(n+1)an
2
，且=1，设Cn=
an
an+1
+
an+1
an
，数列﹛Cn﹜的前n项和为Tn．
（1）求数列﹛an﹜的通项公式；
（2）求证：对任意正整数n，不等式2n＜Tn＜2n+1恒成立．
已知关于x的不等式|x+1|+|2x-1|＜|m-1|+|m-2|有解，求m的取值范围．
函数y=lg（ax+1）在（-∞，1）上单调递减，求a的取值范围．
已知点A（0，2），B（2，0）若点C在函数y=x2的图象上，则使△ABC面积为2的点C的个数是
 
．
若-3＜a＜b＜2，则a-b的取值范围是
 
．
已知0＜t≤
1
4
，那么
1
t
-t的最小值是（　　）
A、
15
4
B、
63
8
C、2
D、-2
已知椭圆：
x2
10-m
+
y2
m-2
=1的焦距为4，则m等于（　　）
A、4B、8
C、4或8D、以上均不对
设圆C1：（x-1）2+y2=1与圆C2：（x-3）2+（y-2）2=1，点P为一动点，由点P作圆C1与圆C2的切线PA，PB，切点分别为A，B．若|PA|=|PB|，则点P的轨迹方程为（　　）
A、x+y-3=0
B、x+y+3=0
C、x-y+3=0
D、x-y-3=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网