题目内容
已知数列﹛an﹜的前n项和Sn=
,且=1,设Cn=
+
,数列﹛Cn﹜的前n项和为Tn.
(1)求数列﹛an﹜的通项公式;
(2)求证:对任意正整数n,不等式2n<Tn<2n+1恒成立.
| (n+1)an |
| 2 |
| an |
| an+1 |
| an+1 |
| an |
(1)求数列﹛an﹜的通项公式;
(2)求证:对任意正整数n,不等式2n<Tn<2n+1恒成立.
考点:数列与不等式的综合,数列递推式
专题:等差数列与等比数列
分析:(1)由题意利用公式法即可求得
=
,再由累乘法得出数列的通项公式;
(2)由(1)得Cn=
+
=
+
=2+
-
,利用裂项法求得Tn=2n+1-
,即可得出证明.
| an |
| an-1 |
| n |
| n-1 |
(2)由(1)得Cn=
| an |
| an+1 |
| an+1 |
| an |
| n |
| n+1 |
| n+1 |
| n |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
解答:
解:(1)∵Sn=
,
∴2sn=(n+1)an,①
n≥2时,2sn-1=nan-1,②
∴由①-②得,2an=(n+1)an-nan-1,
∴
=
,
∴an=a1•
…
=1×
×
×…×
=n,
∴an=n.
(2)由(1)得Cn=
+
=
+
=2+
-
,
∴Tn=c1+c2+…+cn=2n+1-
+
-
+…+
-
=2n+1-
,
∵0<1-
=
<1,
∴2n<Tn<2n+1.
| (n+1)an |
| 2 |
∴2sn=(n+1)an,①
n≥2时,2sn-1=nan-1,②
∴由①-②得,2an=(n+1)an-nan-1,
∴
| an |
| an-1 |
| n |
| n-1 |
∴an=a1•
| a2 |
| a1 |
| an |
| an-1 |
| 2 |
| 1 |
| 3 |
| 2 |
| n |
| n-1 |
∴an=n.
(2)由(1)得Cn=
| an |
| an+1 |
| an+1 |
| an |
| n |
| n+1 |
| n+1 |
| n |
| 1 |
| n |
| 1 |
| n+1 |
∴Tn=c1+c2+…+cn=2n+1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| n+1 |
∵0<1-
| 1 |
| n+1 |
| n |
| n+1 |
∴2n<Tn<2n+1.
点评:本题主要考查数列通项公式的求法及裂项相消法求数列的和等知识,考查学生的运算求解能力,属于中档题.

练习册系列答案
相关题目
如图给出的是计算
+
+
+…+
的值的一个程序框图,其中判断框内应填入的条件是( )
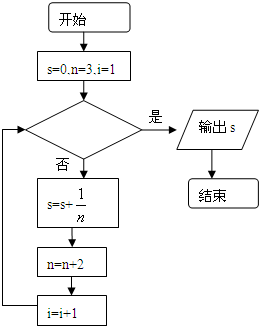
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 7 |
| 1 |
| 21 |

| A、i>10? |
| B、i<10? |
| C、i>20? |
| D、i<20? |
设x,y满足约束条件
,若目标函数z=abx+y(a>0,b>0)的最大值为8,则(a2+b2)-10(a+b)的最小值为( )
|
| A、-32 | B、-33 |
| C、-34 | D、-35 |
从区间[-1,4]上随机取一个数x,则x∈[0,2]的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
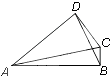 如图,在四边形ABCD中,AB⊥BC,AD⊥DC.若
如图,在四边形ABCD中,AB⊥BC,AD⊥DC.若| AB |
| a |
| AD |
. |
| b |
| AC |
| BD |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|