题目内容
1.已知全集U=R,A={x|x≥3},B={x|x2-8x+7≤0},C={x|x≥a-1}.(Ⅰ)求A∩B,A∪(∁UB);
(Ⅱ)若A∪C=A,求实数a的取值范围.
分析 (Ⅰ)化简集合A,B能求出A∩B,求出CRB,再求A∪(CUB).
(Ⅱ)由A⊆C,能求出a的取值范围.
解答 解:(Ⅰ)A={x|x≥3}=[3,+∞),B={x|x2-8x+7≤0}=[1,7],
∴A∩B=[3,7],
∴∁UB=(-∞,1)∪(7,+∞),
∴A∪(∁UB)=(-∞,1)∪[3,+∞),
(Ⅱ),∵A∪C=A,
∴C⊆A,
∴a-1≥3,
∴a≥4
点评 本题考查集合的交、并、补集的混合运算,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.从1,2,3,4,5中任取三个数,则这三个数成递增的等差数列的概率为( )
| A. | $\frac{3}{10}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{5}$ |
6.下列四组中的f(x),g(x),表示同一个函数的是( )
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x-1,g(x)=$\frac{x^2}{x}$-1 | ||
| C. | f (x)=x2,g(x)=($\sqrt{x}$)4 | D. | f(x)=|x|,g(x)=$\sqrt{x^2}$ |
11.函数$y={(\frac{1}{3})^{|x|}}-1$的值域是( )
| A. | [1,+∞) | B. | [0,+∞) | C. | (-∞,0] | D. | (-1,0] |
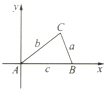 补全用解析法证明余弦定理的过程.
补全用解析法证明余弦定理的过程.