已知:a＞0.b＞0.a+4b=4(1)求ab的最大值,(2)求$\frac{1}{a}$+$\frac{4}{b}$的最小值．题目和参考答案——青夏教育精英家教网—

题目内容

13．已知：a＞0，b＞0，a+4b=4
（1）求ab的最大值；
（2）求$\frac{1}{a}$+$\frac{4}{b}$的最小值．

分析（1）利用基本不等式的性质即可得出．
（2）变形$\frac{1}{a}$+$\frac{4}{b}$=$\frac{1}{4}$（a+4b）$（\frac{1}{a}+\frac{4}{b}）$=$\frac{1}{4}$$（1+16+\frac{4b}{a}+\frac{4a}{b}）$，利用基本不等式的性质即可得出．

解答解：（1）∵a＞0，b＞0，∴a+4b=4≥2$\sqrt{a•4b}$，化为ab≤1，当且仅当a=2，b=$\frac{1}{2}$时取等号．
∴ab的最大值为1．
（2）∵a＞0，b＞0，∴$\frac{1}{a}$+$\frac{4}{b}$=$\frac{1}{4}$（a+4b）$（\frac{1}{a}+\frac{4}{b}）$=$\frac{1}{4}$$（1+16+\frac{4b}{a}+\frac{4a}{b}）$≥$\frac{1}{4}（17+4×2\sqrt{\frac{b}{a}×\frac{a}{b}}）$=$\frac{25}{4}$，当且仅当a=b=$\frac{4}{5}$时取等号．
∴$\frac{1}{a}$+$\frac{4}{b}$的最小值为$\frac{25}{4}$．

点评本题考查了基本不等式的性质、“乘1法”，考查了推理能力与计算能力，属于中档题．

练习册系列答案

4．（1）求不等式a^2x-1＞a^x+2（a＞0，且a≠1）中x的取值范围（用集合表示）．
（2）已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=$\sqrt{x}$+1，求函数f（x）的解析式．

1．函数f（x）=2^|x|的定义域为[a，b]，值域为[1，4]，方程b=g（a）表示的图形可以是（　　）

8．已知幂函数f（x）=（m²-3m+3）x^m+1为偶函数，g（x）=log_a[f（x）-ax]（a＞0且a≠1）．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若g（x）在区间（2，3）上为增函数，求实数a的取值范围．

18．下列结论正确的是（　　）

	A．	当x＞0且x≠1时，$lgx+\frac{1}{lgx}≥2$		B．	当x＞0时，$\sqrt{x}+\frac{1}{{\sqrt{x}}}≥2$
	C．	当x≥2时，$x+\frac{1}{x}≥2$		D．	当0＜x≤2时，$x-\frac{1}{x}$无最大值

3．已知函数f（x）=alnx+ax²+bx，（a，b∈R）．
（1）设a=1，f（x）在x=1处的切线过点（2，6），求b的值；
（2）设b=a²+2，求函数f（x）在区间[1，4]上的最大值；
（3）定义：一般的，设函数g（x）的定义域为D，若存在x₀∈D，使g（x₀）=x₀成立，则称x₀为函数g（x）的不动点．设a＞0，试问当函数f（x）有两个不同的不动点时，这两个不动点能否同时也是函数f（x）的极值点？

20．

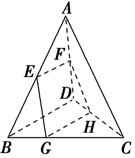如图所示，在空间四边形ABCD中，E，F分别为AB，AD的中点，G，H分别在BC，CD上，且BG：GC=DH：HC=1：2，求证：
（1）E，F，G，H四点共面；
（2）EG与HF的交点在直线AC上．

1．已知全集U=R，A={x|x≥3}，B={x|x²-8x+7≤0}，C={x|x≥a-1}．
（Ⅰ）求A∩B，A∪（∁_UB）；
（Ⅱ）若A∪C=A，求实数a的取值范围．

试题分类