题目内容
10.已知a>0且满足不等式22a+1>25a-2.(1)求实数a的取值范围.
(2)求不等式loga(2x-1)<loga(7-5x).
(3)若函数y=loga(2x-1)在区间[1,3]有最小值为-2,求实数a值.
分析 (1)根据指数函数的单调性解不等式即可求实数a的取值范围.
(2)根据对数函数的单调性求不等式loga(3x+1)<loga(7-5x).
(3)根据复合函数的单调性以及对数的性质即可求出a的值.
解答 解:(1)∵22a+1>25a-2.
∴2a+1>5a-2,即3a<3,
∴a<1.
(2)∵a>0,a<1,∴0<a<1,
∵loga(2x-1)<loga(7-5x).
∴等价为$\left\{\begin{array}{l}{2x-1>0}\\{7-5x>0}\\{2x-1>7-5x}\end{array}\right.$,
∴$\frac{8}{7}$<x<$\frac{7}{5}$,
即不等式的解集为($\frac{8}{7}$,$\frac{7}{5}$).
(3)∵0<a<1,
∴函数y=loga(2x-1)在区间[1,3]上为减函数,
∴当x=3时,y有最小值为-2,
即loga5=-2=logaa-2,
∴a-2=5,
解得a=$\frac{\sqrt{5}}{5}$.
点评 本题主要考查不等式的解法,利用指数函数和对数函数的单调性是解决本题的关键.

练习册系列答案
相关题目
15.已知二次函数y=x2+bx+c的图象过(1,0)与(3,0),则此函数的单调减区间为( )
| A. | (2,+∞) | B. | (-∞,2) | C. | (3,+∞) | D. | (-∞,3) |
19.设M=2a2-4a,N=a2-2a-3,则有( )
| A. | M<N | B. | M≤N | C. | M>N | D. | M≥N |
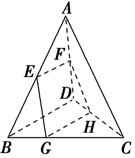 如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2,求证:
如图所示,在空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG:GC=DH:HC=1:2,求证: