题目内容
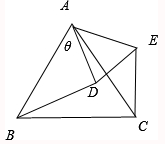如图，已知等边△ABC的边长为2，D为AC的中点，且△ADE也是等边三角形．在△ADE以点A为中心向下转动到稳定位置的过程中，| BD |
| CE |
考点：平面向量数量积的运算
专题：计算题,平面向量及应用
分析：设∠BAD=θ，（0≤θ≤
），则∠CAE=θ，则
•
=（
-
）•（
-
），将其展开，运用向量的数量积的定义，再由两角和差的余弦公式，化简得到
-2cosθ，再由余弦函数的性质，即可得到范围．
| π |
| 3 |
| BD |
| CE |
| AD |
| AB |
| AE |
| AC |
| 5 |
| 2 |
解答：
解：设∠BAD=θ，（0≤θ≤
），
则∠CAE=θ，
则
•
=（
-
）•（
-
）
=
•
-
•
-
•
+
•
=1×1×cos
-1×2×cos（
-θ）-2×1×cos（
+θ）+2×2×cos
=
-2（
cosθ+
sinθ+
cosθ-
sinθ）=
-2cosθ，
由于0≤θ≤
，则
≤cosθ≤1，
则
≤
-2cosθ≤
．
故答案为：[
，
]．
设∠BAD=θ，（0≤θ≤| π |
| 3 |
则∠CAE=θ，
则
| BD |
| CE |
| AD |
| AB |
| AE |
| AC |
=
| AD |
| AE |
| AD |
| AC |
| AB |
| AE |
| AB |
| AC |
=1×1×cos
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=
| 5 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 5 |
| 2 |
由于0≤θ≤
| π |
| 3 |
| 1 |
| 2 |
则
| 1 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
故答案为：[
| 1 |
| 2 |
| 3 |
| 2 |
点评：本题考查平面向量的数量积的定义，考查三角函数的化简和求最值，考查运算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
顶点在坐标原点，对称轴为坐标轴且经过点（-2，3）的抛物线方程是（ ）
A、y2=
| ||||
B、x2=
| ||||
C、y2=-
| ||||
D、y2=-
|
把函数y=sin（2x-
）的图象向左平移
个单位，所得图象的函数解析式是（ ）
| π |
| 4 |
| π |
| 6 |
A、y=sin（2x-
| ||
B、y=sin（2x-
| ||
C、y=sin（2x-
| ||
D、y=sin（2x+
|
对于命题“正方形的四个内角相等”，下面判断正确的是（ ）
| A、所给命题为假 |
| B、它的逆否命题为真 |
| C、它的逆命题为真 |
| D、它的否命题为真 |