题目内容
设
=(-2,m),
=(n,1),
=(5,-1),若A、B、C三点共线,且
⊥
,则m+n的值是 .
| OA |
| OB |
| OC |
| OA |
| OB |
考点:数量积判断两个平面向量的垂直关系
专题:平面向量及应用
分析:由已知得-2n+m=0,且
=
,由此能求出m+n的值.
| m+1 |
| -2-5 |
| 2 |
| n-5 |
解答:
解:∵
=(-2,m),
=(n,1),
=(5,-1),
A、B、C三点共线,且
⊥
,
∴-2n+m=0,解得m=2n,
且
=
,
解得n=3,m=6或n=
,m=3.
∴m+n=9或m+n=
.
故答案为:9或
.
| OA |
| OB |
| OC |
A、B、C三点共线,且
| OA |
| OB |
∴-2n+m=0,解得m=2n,
且
| m+1 |
| -2-5 |
| 2 |
| n-5 |
解得n=3,m=6或n=
| 3 |
| 2 |
∴m+n=9或m+n=
| 9 |
| 2 |
故答案为:9或
| 9 |
| 2 |
点评:本题考查两数和的求法,是基础题,解题时要认真审题,注意平行和向量垂直的性质的合理运用.

练习册系列答案
相关题目
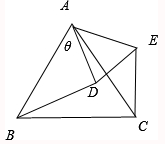 如图,已知等边△ABC的边长为2,D为AC的中点,且△ADE也是等边三角形.在△ADE以点A为中心向下转动到稳定位置的过程中,
如图,已知等边△ABC的边长为2,D为AC的中点,且△ADE也是等边三角形.在△ADE以点A为中心向下转动到稳定位置的过程中,