题目内容
把函数y=sin(2x-
)的图象向左平移
个单位,所得图象的函数解析式是( )
| π |
| 4 |
| π |
| 6 |
A、y=sin(2x-
| ||
B、y=sin(2x-
| ||
C、y=sin(2x-
| ||
D、y=sin(2x+
|
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:根据三角函数图象平移的法则,写出函数图象向左平移
个单位,图象对应的函数解析式即可.
| π |
| 6 |
解答:
解:函数y=sin(2x-
)的图象向左平移
个单位,
所得图象的函数解析式是y=sin(2(x+
)-
),
即y=sin(2x+
-
)=sin(2x+
).
故选:D.
| π |
| 4 |
| π |
| 6 |
所得图象的函数解析式是y=sin(2(x+
| π |
| 6 |
| π |
| 4 |
即y=sin(2x+
| π |
| 3 |
| π |
| 4 |
| π |
| 12 |
故选:D.
点评:本题考查了三角函数图象平移的问题,解题时应明确图象平移的方法是什么(即左+右-),是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
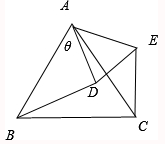 如图,已知等边△ABC的边长为2,D为AC的中点,且△ADE也是等边三角形.在△ADE以点A为中心向下转动到稳定位置的过程中,
如图,已知等边△ABC的边长为2,D为AC的中点,且△ADE也是等边三角形.在△ADE以点A为中心向下转动到稳定位置的过程中,