题目内容
已知λ1>0,λ2>0,
、
是一组基底,且
=λ1
+λ2
,则
与
,
与
(填共线或不共线).
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| a |
| e1 |
| a |
| e2 |
考点:向量的共线定理
专题:平面向量及应用
分析:利用共面向量的基底意义、共线向量定理即可得出.
解答:
解:∵λ1>0,λ2>0,
、
是一组基底,且
=λ1
+λ2
,
则
与
不共线,
与
不共线.
故答案为:不共线,不共线.
| e1 |
| e2 |
| a |
| e1 |
| e2 |
则
| a |
| e1 |
| a |
| e2 |
故答案为:不共线,不共线.
点评:本题考查了共面向量的基底意义、共线向量定理,考查了推理能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设命题甲为:点P的坐标适合方程f(x,y)=0;命题乙:点P在曲线C上;命题丙:点Q坐标不适合f(x,y)=0;命题丁:点Q不在曲线C上.已知甲是乙的必要不充分条件,那么丙是丁的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
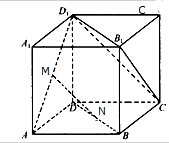 如图所示,在正方体ABCD-A1B1C1D1中,已知正方体的棱长为
如图所示,在正方体ABCD-A1B1C1D1中,已知正方体的棱长为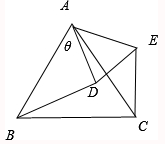 如图,已知等边△ABC的边长为2,D为AC的中点,且△ADE也是等边三角形.在△ADE以点A为中心向下转动到稳定位置的过程中,
如图,已知等边△ABC的边长为2,D为AC的中点,且△ADE也是等边三角形.在△ADE以点A为中心向下转动到稳定位置的过程中,