题目内容
对于定义域为R的函数f(x)=
(a为实常数).
(1)若f(1)=
,求a的值;
(2)当a取(1)中所确定的值,求f(x)的值域;
(3)若f(x)值域为[-1,4],求a.
| 4x-a |
| x2+1 |
(1)若f(1)=
| 1 |
| 2 |
(2)当a取(1)中所确定的值,求f(x)的值域;
(3)若f(x)值域为[-1,4],求a.
考点:函数的值域,函数的值
专题:计算题,函数的性质及应用
分析:(1)由题意,代入函数内求a即可;
(2)利用判别式法求值域;
(3)由判别式法求参数a.
(2)利用判别式法求值域;
(3)由判别式法求参数a.
解答:
解:(1)由题意,
f(1)=
=
,则a=3.
(2)令y=f(x)=
,
则可化为:yx2-4x+y+3=0,
当y=0时,方程有解;
当y≠0时,△=16-4y(y+3)≥0,
解得,-4≤y≤1,
f(x)的值域为[-4,1].
(3)令y=f(x)=
,
则可化为:yx2-4x+y+a=0,
△=16-4y(y+a)=0,的两个解为-1,4;
则4+(a-1)=0,
解得,a=-3.
f(1)=
| 4-a |
| 1+1 |
| 1 |
| 2 |
(2)令y=f(x)=
| 4x-3 |
| x2+1 |
则可化为:yx2-4x+y+3=0,
当y=0时,方程有解;
当y≠0时,△=16-4y(y+3)≥0,
解得,-4≤y≤1,
f(x)的值域为[-4,1].
(3)令y=f(x)=
| 4x-a |
| x2+1 |
则可化为:yx2-4x+y+a=0,
△=16-4y(y+a)=0,的两个解为-1,4;
则4+(a-1)=0,
解得,a=-3.
点评:本题考查了函数的值域的求法及其应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
给出下面几个问题:
①三个朋友合影留念
②用1,2,3三个数字中任选两个数相加求和
③从40名学生中选3人参加代表会
④从40名学生中选3人分别担任班长,团支部书记和生活委员
其中属于排列问题的是( )
①三个朋友合影留念
②用1,2,3三个数字中任选两个数相加求和
③从40名学生中选3人参加代表会
④从40名学生中选3人分别担任班长,团支部书记和生活委员
其中属于排列问题的是( )
| A、①② | B、②④ | C、①③ | D、①④ |
设命题甲为:点P的坐标适合方程f(x,y)=0;命题乙:点P在曲线C上;命题丙:点Q坐标不适合f(x,y)=0;命题丁:点Q不在曲线C上.已知甲是乙的必要不充分条件,那么丙是丁的( )条件.
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
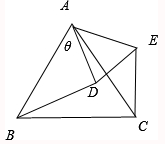 如图,已知等边△ABC的边长为2,D为AC的中点,且△ADE也是等边三角形.在△ADE以点A为中心向下转动到稳定位置的过程中,
如图,已知等边△ABC的边长为2,D为AC的中点,且△ADE也是等边三角形.在△ADE以点A为中心向下转动到稳定位置的过程中,