题目内容
已知两个正数x，y满足x+4y+5-xy=0，则xy取最小值时x= ，y= ．
考点：基本不等式在最值问题中的应用,函数的最值及其几何意义
专题：综合题,不等式的解法及应用
分析：将方程变形x+4y=xy-5，再由基本不等式转化为关于xy的不等式，根据x和y范围进行求解，结合等号成立的条件和xy的最小值，求出此时x和y对应的值．
解答：
解：∵x+4y+5-xy=0，∴x+4y=xy-5①，
∵x，y是正数，∴x+4y≥4
，当且仅当x=4y时等号成立，
代入①式得，xy-5≥4
，即xy-4
-5≥0，解得
≥5或
≤-1（舍去），
∴xy取最小值25，
∵x=4y，
∴解得x=10，y=2.5，
故答案为：10，2.5．
∵x，y是正数，∴x+4y≥4
| xy |
代入①式得，xy-5≥4
| xy |
| xy |
| xy |
| xy |
∴xy取最小值25，
∵x=4y，
∴解得x=10，y=2.5，
故答案为：10，2.5．
点评：本题考查了基本不等式的应用，利用基本不等式将方程转化为不等式，再进行求解，注意“一正、二定、三相等”的验证．
练习册系列答案
53天天练系列答案
相关题目
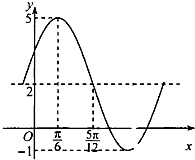已知函数f（x）=Asin（ωx+φ）+b（A、ω＞0，0＜φ＜π，b为常数）一段图象如图所示．
设函数f（x）=|x2-4x-5|．方程ax2+2x+1=0恰有一个负实根，则a的取值范围为（ ）
| A、a＜0 | B、a≤0 |
| C、a＞0 | D、a=0 |