题目内容
求不等式ax+1＜a2+x（a∈R）的解集．
考点：其他不等式的解法
专题：计算题,不等式的解法及应用
分析：将原不等式化为（a-1）x＜a2-1，对a-1分a-1＞0、a-1=0及a-1＜0三类讨论，即可求得不等式ax+1＜a2+x（a∈R）的解集．
解答：
解：将原不等式化为（a-1）x＜a2-1．
①当a-1＞0，即a＞1时，x＜a+1；
②当a-1＜0，即a＜1时，x＞a+1；
③当a-1=0，即a=1时，不等式无解．
综上所述，
当a＞1时，不等式的解集为{x|x＜a+1}；
当a＜1时，不等式的解集为{x|x＞a+1}；
当a=1时，不等式的解集为∅．
①当a-1＞0，即a＞1时，x＜a+1；
②当a-1＜0，即a＜1时，x＞a+1；
③当a-1=0，即a=1时，不等式无解．
综上所述，
当a＞1时，不等式的解集为{x|x＜a+1}；
当a＜1时，不等式的解集为{x|x＞a+1}；
当a=1时，不等式的解集为∅．
点评：本题考查含参数的一次不等式的解法，着重考查分类讨论思想的应用，考查运算求解能力，属于中档题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
若△ABC的内角A，B，C所对的边分别为a，b，c，且a2=c2-b2+
ba，则∠C=（ ）
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若直线y=kx-1与圆x2+y2=1相交于P、Q两点，且∠POQ=120°（其中Q为原点），则K的值为（ ）
A、
| ||||
B、4，-
| ||||
C、
| ||||
| D、1，-1 |
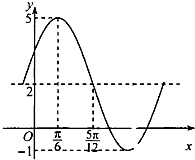已知函数f（x）=Asin（ωx+φ）+b（A、ω＞0，0＜φ＜π，b为常数）一段图象如图所示．