题目内容
如果(x3-
)n的展开式中只有第4项的二项式系数最大，那么展开式中的所有项的系数和是（ ）
| 1 |
| 2x |
A、
| ||
| B、0 | ||
| C、64 | ||
| D、256 |
考点：二项式定理的应用,二项式系数的性质
专题：二项式定理
分析：由二项式系数的性质，结合题意可知，二项展开式共有7项，n=6，二项展开式的所有项的系数和就是在展开式中取x=1的值，则只需在二项式中取x=1即可．
解答：
解：∵(x3-
)n的展开式中只有第4项的二项式系数最大，
∴该二项式的展开式共有7项，n=6．
在二项式(x3-
)n中取x=1，得展开式中的所有项的系数和为(13-
)6=(
)6=
．
故选：A．
| 1 |
| 2x |
∴该二项式的展开式共有7项，n=6．
在二项式(x3-
| 1 |
| 2x |
| 1 |
| 2×1 |
| 1 |
| 2 |
| 1 |
| 64 |
故选：A．
点评：本题考查了二项式系数的性质，解答的关键是区分二项式系数和项的系数，考查了学生灵活处理问题和解决问题的能力，是中档题．
练习册系列答案
春雨教育同步作文系列答案
相关题目
已知随机变量X～B（6，0.4），则当η=-2X+1时，D（η）=（ ）
| A、-1.88 | B、-2.88 |
| C、5.76 | D、6.76 |
点P是函数y=x2-2lnx的图象上任意一点，则点P到直线y=3x-1的最小距离是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若直线y=kx-1与圆x2+y2=1相交于P、Q两点，且∠POQ=120°（其中Q为原点），则K的值为（ ）
A、
| ||||
B、4，-
| ||||
C、
| ||||
| D、1，-1 |
掷两颗均匀的大小不同的骰子，记“两颗骰子的点数和为10”为事件A，“小骰子出现的点数大于大骰子出现的点数”为事件B，则P（B|A）为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
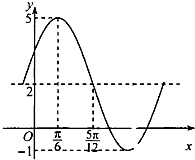已知函数f（x）=Asin（ωx+φ）+b（A、ω＞0，0＜φ＜π，b为常数）一段图象如图所示．