题目内容
已知函数f（x）的图象与g（x）=
的图象关于y=x对称，求f（2）．
| 2x+1 |
| 4x+1 |
考点：反函数
专题：函数的性质及应用
分析：由于函数f（x）的图象与g（x）=
的图象关于y=x对称，因此函数f（x）是g（x）的反函数，求出即可．
| 2x+1 |
| 4x+1 |
解答：
解：由y=g（x）=
(x≠-
)，解出x=
，将x与y互换可得y=
(x≠
)．
∵函数f（x）的图象与g（x）=
的图象关于y=x对称，
∴f（x）=
(x≠
)．
∴f（2）=
=-
．
| 2x+1 |
| 4x+1 |
| 1 |
| 4 |
| 1-y |
| 4y-2 |
| 1-x |
| 4x-2 |
| 1 |
| 2 |
∵函数f（x）的图象与g（x）=
| 2x+1 |
| 4x+1 |
∴f（x）=
| 1-x |
| 4x-2 |
| 1 |
| 2 |
∴f（2）=
| 1-2 |
| 4×2-2 |
| 1 |
| 6 |
点评：本题考查了互为反函数的性质，属于基础题．
练习册系列答案
相关题目
在△ABC中，sinA=sinB是A=B的（ ）
| A、充要条件 |
| B、充分非必要条件 |
| C、必要非充分条件 |
| D、既非充分条件又非必要条件 |
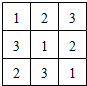（1）如图，将1，2，3填入3×3的方格中，要求每行、每列都没有重复数字，右面是一种填法，则不同的填写方法共有几种？（用数字作答）．