题目内容
观察如图三角形数表:

假设第n行的第二个数为an(n≥2,n∈N*).
(1)依次写出第八行的所有8个数字;
(2)归纳出an+1的关系式,并求出an的通项公式.

假设第n行的第二个数为an(n≥2,n∈N*).
(1)依次写出第八行的所有8个数字;
(2)归纳出an+1的关系式,并求出an的通项公式.
考点:数列的函数特性,归纳推理
专题:等差数列与等比数列
分析:(1)其规律:每行除首末数字与行数相同外,每个数等于其肩上两数字之和.
(2)由已知:an+1=n+an(n≥2,n∈N+),再利用“累加求和”即可得出.
(2)由已知:an+1=n+an(n≥2,n∈N+),再利用“累加求和”即可得出.
解答:
解:(1)其规律:每行除首末数字与行数相同外,每个数等于其肩上两数字之和.
∴第八行为:8,29,63,91,91,63,29,8.
(2)由已知:an+1=n+an(n≥2,n∈N+),
∴an-an-1=n-1,an-1-an-2=n-2,…a4-a3=3,a3-a2=2,a2=2
将以上各式相加的:an=2+2+3+…(n-2)+(n-1)=
∴an的通项公式为:an=
(n≥2,n∈N+).
∴第八行为:8,29,63,91,91,63,29,8.
(2)由已知:an+1=n+an(n≥2,n∈N+),
∴an-an-1=n-1,an-1-an-2=n-2,…a4-a3=3,a3-a2=2,a2=2
将以上各式相加的:an=2+2+3+…(n-2)+(n-1)=
| n2-n+2 |
| 2 |
∴an的通项公式为:an=
| n2-n+2 |
| 2 |
点评:本题考查了通过观察、分析、猜想、归纳得出数列的通项公式、“累加求和”方法、等差数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
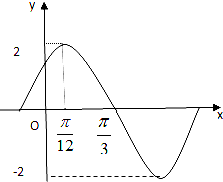 已知函数f(x)=Acos(ωx+φ),(A>0,ω>0,|φ|<
已知函数f(x)=Acos(ωx+φ),(A>0,ω>0,|φ|<