Question

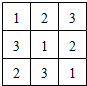（1）如图，将1，2，3填入3×3的方格中，要求每行、每列都没有重复数字，右面是一种填法，则不同的填写方法共有几种？（用数字作答）．
（2）有4张分别标有数字1，2，3，4的红色卡片和4张分别标有数字1，2，3，4的蓝色卡片，从这8张卡片中取出4张卡片排成一行．如果取出的4张卡片所标的数字之和等于10，则不同的排法共有

 

种？（用数字作答）．
（3）用1，2，3，4，5，6组成六位数（没有重复数字），要求任何相邻两个数字的奇偶性不同，且1和2相邻，这样的六位数的个数是多少？（用数字作答）．

Answer 1

考点：计数原理的应用

专题：排列组合

分析：（1）填好第一行和第一列，其他的行和列就确定，因此只要选好第一行的顺序再确定第一列的顺序，就可以得到符合要求的排列．
（2）根据题意，分析可得，数字之和为10的情况有4，4，1，1；4，3，2，1； 3，3，2，2；再依次求得每种情况下的排法数目，进而由加法原理，相加可得答案．
（3）欲求可组成符合条件的六位数的个数，只须利用分步计数原理分三步计算：第一步：先将3、5排列，第二步：再将4、6插空排列，第三步：将1、2放到3、5、4、6形成的空中即可．

解答： 解：（1）填好第一行和第一列，其他的行和列就确定，则不同的填写方法共A₃³A₂²=12种，
（2）数字之和为10的情况有4，4，1，1；4，3，2，1； 3，3，2，2；
取出的卡片数字为4，4，1，1时；有A₄⁴种不同排法；
取出的卡片数字为3，3，2，2时；有A₄⁴种不同排法；
取出的卡片数字为4，3，2，1时；每个数字都有两种不同的取法，则有2⁴A₄⁴种不同排法；
所以共有2A₄⁴+2⁴A₄⁴=18A₄⁴=432种不同排法．
故答案为：432
（3）解析：可分三步来做这件事：
第一步：先将3、5排列，共有A₂²种排法；
第二步：再将4、6插空排列，共有2A₂²种排法；
第三步：将1、2放到3、5、4、6形成的空中，共有C₅¹种排法．
由分步乘法计数原理得共有A₂²•2A₂²•C₅¹=40（种）．

点评：本题主要考查了分类和分步计数原理，关键是分清是分类还是分步，属于中档题．