题目内容
在1,2,…,7这7个自然数中,任取3个不同的数.
(1)求这3个数中至少有1个是偶数的概率;
(2)设ξ为这3个数中两数相邻的组数(例如:若取出的数为1,2,3,则有两组相邻的数1,2和2,3,此时ξ的值是2).求随机变量ξ的分布列及其数学期望Eξ.
(1)求这3个数中至少有1个是偶数的概率;
(2)设ξ为这3个数中两数相邻的组数(例如:若取出的数为1,2,3,则有两组相邻的数1,2和2,3,此时ξ的值是2).求随机变量ξ的分布列及其数学期望Eξ.
考点:离散型随机变量及其分布列,离散型随机变量的期望与方差
专题:概率与统计
分析:(1)本题是一个等可能事件的概率,试验发生包含的事件是满足条件的事件是至少有一个是偶数,C73-
种结果,得到概率.
(2)有可能相邻的:123,124,125,126,127,224,235,236,237,345,346,347,456,457,567.共15个,不包含相邻的数的有35-15=20,根据概率公式求解得当变量为0时表示不包含相邻的数P(ξ=0)=
=
,
当变量为1时表示包含1组相邻的数P(ξ=1)=
=
,当变量为2时表示包含2组相邻的数P(ξ=2)=
=
列出分布列,求解出数学期望即可.
| C | 3 4 |
(2)有可能相邻的:123,124,125,126,127,224,235,236,237,345,346,347,456,457,567.共15个,不包含相邻的数的有35-15=20,根据概率公式求解得当变量为0时表示不包含相邻的数P(ξ=0)=
| 20 |
| 35 |
| 4 |
| 7 |
当变量为1时表示包含1组相邻的数P(ξ=1)=
| 10 |
| 35 |
| 2 |
| 7 |
| 5 |
| 35 |
| 1 |
| 7 |
列出分布列,求解出数学期望即可.
解答:
解::(1)由题意知本题是一个等可能事件的概率,
∵试验发生包含的事件是从7个数字中任取3个,共有C7
=35种结果,
满足条件的事件是至少有一个是偶数,C73-
种结果,
记“这3个数至少有一个是偶数”为事件A,
∴P(A)=1-
=1-
=
,
即3个数中至少有1个是偶数的概率是
.
(2))随机变量ξ为这三个数中两数相邻的组数,
从7个数字中任取3个,共有C73种结果,
有可能相邻的:123,124,125,126,127,234,235,236,237,345,346,347,456,457,567.共15个
不包含相邻的数的有35-15=20
∵则ξ的取值为0,1,2,
当变量为0时表示不包含相邻的数P(ξ=0)=
=
,
当变量为1时表示包含1组相邻的数P(ξ=1)=
=
,
当变量为2时表示包含2组相邻的数P(ξ=2)=
=
随机变量ξ的分布列:
其数学期望Eξ=0×
+1×
+2×
=
∵试验发生包含的事件是从7个数字中任取3个,共有C7
3 |
满足条件的事件是至少有一个是偶数,C73-
| C | 3 4 |
记“这3个数至少有一个是偶数”为事件A,
∴P(A)=1-
| ||
|
| 4 |
| 35 |
| 31 |
| 35 |
即3个数中至少有1个是偶数的概率是
| 31 |
| 35 |
(2))随机变量ξ为这三个数中两数相邻的组数,
从7个数字中任取3个,共有C73种结果,
有可能相邻的:123,124,125,126,127,234,235,236,237,345,346,347,456,457,567.共15个
不包含相邻的数的有35-15=20
∵则ξ的取值为0,1,2,
当变量为0时表示不包含相邻的数P(ξ=0)=
| 20 |
| 35 |
| 4 |
| 7 |
当变量为1时表示包含1组相邻的数P(ξ=1)=
| 10 |
| 35 |
| 2 |
| 7 |
当变量为2时表示包含2组相邻的数P(ξ=2)=
| 5 |
| 35 |
| 1 |
| 7 |
随机变量ξ的分布列:
| ξ | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 4 |
| 7 |
| 2 |
| 7 |
| 1 |
| 7 |
| 4 |
| 7 |
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
从6本不同的数学书和5本不同的英语书中取3本,要求数学书和英语书都要有取到,则不同的取法种数有( )种.
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
(x+1)5展开式的二项式系数的和是( )
| A、6 | B、128 | C、32 | D、64 |
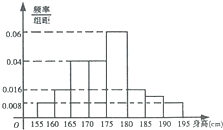 从某校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图:
从某校高三年级800名学生中随机抽取50名测量身高,据测量,被抽取的学生的身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图: