题目内容
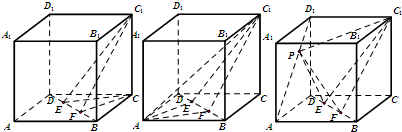
已知正方体ABCD-A1B1C1D1,E,F是BD上的动点,是AD1上的动点,则( )

| A、VC-C1EF=VA-C1EF=VP-C1EF |
| B、VC-C1EF=VA-C1EF<VP-C1EF |
| C、VC-C1EF=VA-C1EF>VP-C1EF |
| D、VC-C1EF<VA-C1EF<VP-C1EF |
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离,空间角
分析:首先利用转换法求出VC-C1EF=VC1-CEF,进一步算出体积VA-C1EF=VC1-AEF=
S△AEF•AA1,最后利用特殊点进行比较,最后求出结果.
| 1 |
| 3 |
解答:
解:如上图(1)VC-C1EF=VC1-CEF=
S△CEF•AA1
如图(2)在平面ABCD中,点A到BD的距离与点C到BD的距离相等.
S△AEF=S△CEF
VA-C1EF=VC1-AEF=
S△AEF•AA1
如图(3)点P是AD1上的点,当点P与A重合时,
VP-C1EF=VA-C1EF
由于A到平面C1EF的距离大于P到平面C1EF的距离
所以:VP-C1EF<VA-C1EF
故选:C
| 1 |
| 3 |
如图(2)在平面ABCD中,点A到BD的距离与点C到BD的距离相等.
S△AEF=S△CEF
VA-C1EF=VC1-AEF=
| 1 |
| 3 |
如图(3)点P是AD1上的点,当点P与A重合时,
VP-C1EF=VA-C1EF
由于A到平面C1EF的距离大于P到平面C1EF的距离
所以:VP-C1EF<VA-C1EF
故选:C
点评:本题考查的知识要点:棱锥的体积公式的应用,几何体的转换问题,及特殊点法的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
利用计算机产生0~1之间的群与随机数a,则事件-
<3a-1<0发生的概率为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
一项“过关游戏”规则规定:在第n关要抛掷一颗骰子n次,如果这n次抛掷所出现的点数的和大于2n”,则算过关,则某人连过前三关的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列命题中的假命题是( )
A、?x∈R,sinx=
| ||||
| B、?x∈R,log2x=1 | ||||
C、?x∈R,(
| ||||
| D、?x∈R,x2≥0 |
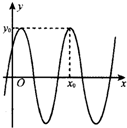 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+