题目内容
关于函数f(x)=
(x≠0),下列说法正确的是 .
①函数f(x)有两个极值点x=±
;
②函数f(x)的值域为(-∞,-2
+a]∪[2
+a,+∞);
③当a≤1时,函数f(x)在[1,+∞)是增函数;
④函数f(x)的图象与x轴有两个公共点的充要条件是a>4或a<0.
| x2+ax+a |
| x |
①函数f(x)有两个极值点x=±
| a |
②函数f(x)的值域为(-∞,-2
| a |
| a |
③当a≤1时,函数f(x)在[1,+∞)是增函数;
④函数f(x)的图象与x轴有两个公共点的充要条件是a>4或a<0.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:求出原函数的导函数,取a=0即可判断①②错误;分a≤0和a>0分别研究函数的单调性判断③正确;由a<0分析原函数的图象的大致情况,由a>0求使函数在x<0时的最大值大于0求解a的范围判断④.
解答:
解:f(x)=
=x+
+a,
f′(x)=1-
=
.
若a=0,则f′(x)=1>0,函数f(x)在(-∞,0),(0,+∞)上为增函数,不存在极值点,命题①错误;
若a=0,函数f(x)=x(x≠0),值域为(-∞,0)∪(0,+∞),命题②错误;
由f′(x)=1-
=
,当a≤0时,f′(x)>0,函数f(x)在[1,+∞)是增函数;
当a>0时,由f′(x)≥0,得x≤-
或x≥
.
若a≤1,则函数f(x)在[1,+∞)是增函数,命题③正确;
当a<0时,函数f(x)在(-∞,0),(0,+∞)上为增函数,
又当x小于0且无限趋于0时,x+
+a>0,当x大于0且无限趋于0时,x+
+a<0,
∴a<0时函数f(x)的图象与x轴有两个公共点.
当a>0时,由y=x+
+a在x<0时的最大值a-2
>0,解得:a>4.
∴函数f(x)的图象与x轴有两个公共点的充要条件是a>4或a<0.
∴正确的命题是③④.
故答案为:③④.
| x2+ax+a |
| x |
| a |
| x |
f′(x)=1-
| a |
| x2 |
| x2-a |
| x2 |
若a=0,则f′(x)=1>0,函数f(x)在(-∞,0),(0,+∞)上为增函数,不存在极值点,命题①错误;
若a=0,函数f(x)=x(x≠0),值域为(-∞,0)∪(0,+∞),命题②错误;
由f′(x)=1-
| a |
| x2 |
| x2-a |
| x2 |
当a>0时,由f′(x)≥0,得x≤-
| a |
| a |
若a≤1,则函数f(x)在[1,+∞)是增函数,命题③正确;
当a<0时,函数f(x)在(-∞,0),(0,+∞)上为增函数,
又当x小于0且无限趋于0时,x+
| a |
| x |
| a |
| x |
∴a<0时函数f(x)的图象与x轴有两个公共点.
当a>0时,由y=x+
| a |
| x |
| a |
∴函数f(x)的图象与x轴有两个公共点的充要条件是a>4或a<0.
∴正确的命题是③④.
故答案为:③④.
点评:本题考查了利用导数研究函数的单调性,考查了利用导数求函数的极值,考查了学生的逻辑思维能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是( )


| A、7 | ||
B、
| ||
C、
| ||
D、
|
我班制定了数学学习方案:星期一和星期日分别解决4个数学问题,且从星期二开始,每天所解决问题的个数与前一天相比,要么“多一个”要么“持平”要么“少一个”.在一周中每天所解决问题个数的不同方案共有( )
| A、50种 | B、51种 |
| C、140种 | D、141种 |
已知正方体ABCD-A1B1C1D1,E,F是BD上的动点,是AD1上的动点,则( )
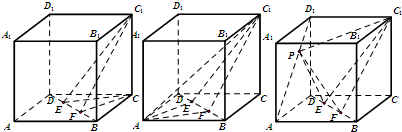

| A、VC-C1EF=VA-C1EF=VP-C1EF |
| B、VC-C1EF=VA-C1EF<VP-C1EF |
| C、VC-C1EF=VA-C1EF>VP-C1EF |
| D、VC-C1EF<VA-C1EF<VP-C1EF |