题目内容
已知f(x)=ax2+bx+2015满足f(-1)=f(3),则f(2)= .
考点:二次函数的性质
专题:函数的性质及应用
分析:由题意应对a进行分类:a=0时和a≠0时,再由条件分别判断出函数为常函数和二次函数的对称轴,再由函数的性质求值.
解答:
解:①当a=0时,
∵f(-1)=f(3),
∴函数f(x)是常函数,即a=b=0,
∴f(x)=2015,则f(2)=2015,
②当a≠0时,则函数f(x)是二次函数,
∵f(-1)=f(3),
∴f(x)的对称轴是:x=1,
∴f(2)=f(0)=2015,
综上得,f(0)=2015,
故答案为:2015
∵f(-1)=f(3),
∴函数f(x)是常函数,即a=b=0,
∴f(x)=2015,则f(2)=2015,
②当a≠0时,则函数f(x)是二次函数,
∵f(-1)=f(3),
∴f(x)的对称轴是:x=1,
∴f(2)=f(0)=2015,
综上得,f(0)=2015,
故答案为:2015
点评:本题考查了利用常函数和二次函数的性质求值,特别再求出对称轴后,不用a和b的值直接由f(2)=f(0)求解,易错点易忘对a进行讨论.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
已知正方体ABCD-A1B1C1D1,E,F是BD上的动点,是AD1上的动点,则( )
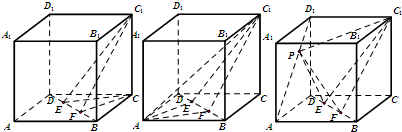

| A、VC-C1EF=VA-C1EF=VP-C1EF |
| B、VC-C1EF=VA-C1EF<VP-C1EF |
| C、VC-C1EF=VA-C1EF>VP-C1EF |
| D、VC-C1EF<VA-C1EF<VP-C1EF |
已知x>1,则函数f(x)=4x+
+1的最小值是( )
| 1 |
| x-1 |
| A、7 | B、9 | C、11 | D、13 |