题目内容
设a,b,c为正数,且满足a2+b2=c2,则log2(1+
)+log2(1+
)= .
| b+c |
| a |
| a-c |
| b |
考点:对数的运算性质
专题:函数的性质及应用
分析:根据对数的运算性质化简计算即可.
解答:
解:∵a、b、c为正数,且满足a2+b2=c2.
∴log2(1+
)+log2(1+
),
=log2(1+
)•(1+
),
=log2(
),
=log22,
=1,
故答案为:1
∴log2(1+
| b+c |
| a |
| a-c |
| b |
=log2(1+
| b+c |
| a |
| a-c |
| b |
=log2(
| 2ab+a2+b2-c2 |
| ab |
=log22,
=1,
故答案为:1
点评:本题考查对数值的求法,注意对数运算性质的合理运用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如果
<σ<
,那么下列不等式成立的是( )
| π |
| 4 |
| π |
| 2 |
| A、cosσ<sinσ<tanσ |
| B、tanσ<sinσ<cosσ |
| C、sinσ<cosσ<tanσ |
| D、cosσ<tanσ<sinσ |
函数y=
的最大值是( )
| 1 |
| 3+2sinx+cosx |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
复数
的模是( )
| 2-i |
| 1+i |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,点D是边BC的中点,点E是线段AD的中点,连接CE交边AB于点F,若
=λ
,则实数λ的值是( )
| AB |
| AF |
A、
| ||
| B、4 | ||
C、
| ||
| D、3 |
sin110°cos25°-sin20°sin25°=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
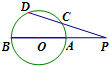 如图所示,AB是半径等于3的⊙O的直径,CD是⊙O的弦,BA,DC的延长线交于点P,若PA=4,PC=5,则DC=
如图所示,AB是半径等于3的⊙O的直径,CD是⊙O的弦,BA,DC的延长线交于点P,若PA=4,PC=5,则DC=