题目内容
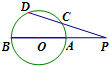 如图所示,AB是半径等于3的⊙O的直径,CD是⊙O的弦,BA,DC的延长线交于点P,若PA=4,PC=5,则DC=
如图所示,AB是半径等于3的⊙O的直径,CD是⊙O的弦,BA,DC的延长线交于点P,若PA=4,PC=5,则DC=考点:与圆有关的比例线段
专题:立体几何
分析:由已知中AB是半径等于3的⊙O的直径,可得PB的长,结合割线定理:PA•PB=PC•PD,先求出PD的长,进而可得答案.
解答:
解:∵AB是半径等于3的⊙O的直径,PA=4,PC=5,
∴PB=4+2×3=10,
由割线定理可得:
PA•PB=PC•PD,
即4×10=5PD,
解得:PD=8.
故DC=PD-PC=3,
故答案为:3
∴PB=4+2×3=10,
由割线定理可得:
PA•PB=PC•PD,
即4×10=5PD,
解得:PD=8.
故DC=PD-PC=3,
故答案为:3
点评:本题考查的知识点是与圆有关的比例线段,熟练掌握割线定理,并由之得到PA•PB=PC•PD,是解答的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
函数f(x)=-x2+8x-16在区间[3,5]上( )
| A、没有零点 | B、有一个零点 |
| C、有两个零点 | D、无数个零点 |
已知(x-
)6的展开式中常数项为-160,则常数a=( )
| 2a |
| x |
A、
| ||
B、-
| ||
| C、1 | ||
| D、-1 |
下列计算不正确的是( )
| A、log3243=log335=5log33=5×1=5 | ||||
B、log510-log52=log5
| ||||
| C、lg2+lg5=lg(2×5)=lg10=1 | ||||
D、log8(8×4)=log88+log84=1+
|