题目内容
在平面直角坐标系xoy中,P(x0,y0)是椭圆C:
+
=1上任意一点,F是椭圆C的左焦点,直线l的方程为x0x+3y0y-6=0.
(1)求证:直线l与椭圆C有唯一公共点;
(2)设点Q与点F关于直线l对称,当点P在椭圆上运动时,判断直线PQ是否过定点,若直线PQ过定点,求出此定点的坐标;若直线PQ不过定点,说明理由.
| x2 |
| 6 |
| y2 |
| 2 |
(1)求证:直线l与椭圆C有唯一公共点;
(2)设点Q与点F关于直线l对称,当点P在椭圆上运动时,判断直线PQ是否过定点,若直线PQ过定点,求出此定点的坐标;若直线PQ不过定点,说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)联立方程组,证明原方程组有只有一组解,即可得出结论;
(2)求出过点F且与直线l垂直的直线方程与直线l的方程联立,求出Q的坐标,分类讨论,求出直线PQ的方程,即可得出结论.
(2)求出过点F且与直线l垂直的直线方程与直线l的方程联立,求出Q的坐标,分类讨论,求出直线PQ的方程,即可得出结论.
解答:
(1)证明:联立方程组
,消去y得:(x02+3y02)x2-12x0x+36-18y02=0,
又
+
=1得3y02=6-x02,代入得:x2-2x0x+x02=0,
因为:△=4x02-4x02=0,所以原方程组有只有一组解,
所以直线l与椭圆C有唯一公共点;
(2)解:点F的坐标为(-2,0),过点F且与直线l垂直的直线方程为3y0x-x0y+6y0=0,
解方程组
得
,
所以点Q的坐标是(
,
),
当x0≠2时,kPQ=
,所以直线PQ的方程为y-y0=
(x-x0),
即(x-2)y0-yx0+2y=0,过定点M(2,0).
当x0=2时,y0=±
,此时点Q的坐标为(2,±2
),直线PQ过定点M(2,0),
综上:直线PQ过定点M(2,0).
|
又
| x02 |
| 6 |
| y02 |
| 2 |
因为:△=4x02-4x02=0,所以原方程组有只有一组解,
所以直线l与椭圆C有唯一公共点;
(2)解:点F的坐标为(-2,0),过点F且与直线l垂直的直线方程为3y0x-x0y+6y0=0,
解方程组
|
|
所以点Q的坐标是(
| 4x0-6 |
| 3-x0 |
| 6y0 |
| 3-x0 |
当x0≠2时,kPQ=
| y0 |
| x0-2 |
| y0 |
| x0-2 |
即(x-2)y0-yx0+2y=0,过定点M(2,0).
当x0=2时,y0=±
| ||
| 3 |
| 6 |
综上:直线PQ过定点M(2,0).
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相切问题转化为原方程组有只有一组解,考查直线过定点问题,考查了推理能力和计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设全集U=R,集合A={x|0<x≤2},B={x|x<1},则集合∁U(A∪B)=( )
| A、(-∞,2] |
| B、(-∞,1] |
| C、(2,+∞) |
| D、[2,+∞) |
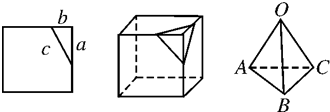
 如图所示,空间中有一直角三角形POA,∠O为直角,OA=4,PO=3,现以其中一直角边PO为轴,按逆时针方向旋转60°后,将A点所在的位置记为B,再按逆时针方向继续旋转120°后,A点所在的位置记为C.
如图所示,空间中有一直角三角形POA,∠O为直角,OA=4,PO=3,现以其中一直角边PO为轴,按逆时针方向旋转60°后,将A点所在的位置记为B,再按逆时针方向继续旋转120°后,A点所在的位置记为C.