题目内容

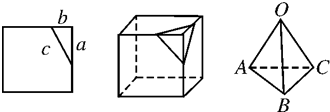
在平面上，用一条直线截正方形的一个角，则截下一个直角三角形按下图所标边长，由勾股定理得c2=a2+b2．设想正方形换成正方体，把截线换成如图的截面，这时从正方体上截下正方体的“一个角”三条侧棱两两垂直的三棱锥O-ABC，若用s1，s2，s3表示三个侧面面积，s4表示截面面积，你类比得到s1，s2，s3，s4之间的关系式为
 
．
考点：类比推理
专题：解题方法,演绎法,推理和证明
分析：从平面图形到空间图形，同时模型不变．
解答： 解：建立从平面图形到空间图形的类比，于是作出猜想：S42=S12+S22+S32
故答案为：S42=S12+S22+S32
点评：本题题主要考查学生的知识量和知识迁移、类比的基本能力．
练习册系列答案
相关题目
在平面直角坐标系xoy中，P（x0，y0）是椭圆C：
x2
6
+
y2
2
=1上任意一点，F是椭圆C的左焦点，直线l的方程为x0x+3y0y-6=0．
（1）求证：直线l与椭圆C有唯一公共点；
（2）设点Q与点F关于直线l对称，当点P在椭圆上运动时，判断直线PQ是否过定点，若直线PQ过定点，求出此定点的坐标；若直线PQ不过定点，说明理由．
已知函数f（x）=cos（2x+
π
3
）+cos2（
π
2
+x）．
（1）求函数f（x）的单调递增区间．
（2）△ABC中，角A、B、C所对的边分别是a、b、c，且f（
c
2
）=-
1
4
，边c=2，∠C为锐角，△ABC的内切圆半径为
3
3
，求△ABC的面积．
设集合A={x|x2-4x-12＞0}，B={x||x-3|＜a}，且-3∈B，则A∪B=
 
．
当对数logx-1（5+4x）有意义时，x的取值范围是
 
．
若
1
1+x2
=a0+a1x+a2x2+a3x3+…+anxn+…，则a3=
 
．
经过点（2，-3）且与椭圆9x2+y2=36共焦点的椭圆方程为
 
．
如图是甲，乙两名同学5次综合测评成绩的茎叶图，则乙的成绩的中位数是
 
，甲乙两人中成绩较为稳定的是
 
．
某几何体的俯视图是正方形，则该几何体不可能是（　　）
A、圆柱B、圆锥
C、三棱柱D、四棱柱

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网