题目内容
已知O为平面ABC内任一点，若A，B，C三点共线，是否存在α，β∈R，使
=α
+β
，其中α+β=1？
| OC |
| OA |
| OB |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：A，B，C三点共线，利用向量共线定理可得：存在实数α使得
=α
，化简整理即可得出．
| BC |
| BA |
解答：
解：∵A，B，C三点共线，
∴存在实数α使得
=α
，
∴
-
=α(
-
)，
化为
=α
+(1-α)
，
令1-α=β，
则
=α
+β
，其中α+β=1．
∴存在α，β∈R，使
=α
+β
，其中α+β=1．
∴存在实数α使得
| BC |
| BA |
∴
| OC |
| OB |
| OA |
| OB |
化为
| OC |
| OA |
| OB |
令1-α=β，
则
| OC |
| OA |
| OB |
∴存在α，β∈R，使
| OC |
| OA |
| OB |
点评：本题查克拉向量共线定理，属于基础题．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
把函数y=sin（2x-
）的图象向左平移
个单位后，所得函数图象的一条对称轴为（ ）
| π |
| 6 |
| π |
| 6 |
| A、x=0 | ||
B、x=
| ||
C、x=-
| ||
D、x=
|
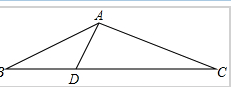如图△ABC中，∠BAC=120°，AB=1，AC=2，D在BC上，且DC=4BD，则AD的长为