题目内容
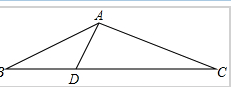如图△ABC中，∠BAC=120°，AB=1，AC=2，D在BC上，且DC=4BD，则AD的长为考点：余弦定理的应用,三角形中的几何计算
专题：解三角形
分析：直接利用已知条件以及余弦定理得求得AD的长即可．
解答：
解：由题意△ABC中，∠BAC=120°，AB=1，AC=2，D在BC上，且DC=4BD，
可得
cosA=
=
BC2=AB2+AC2-2AB•ACcosA=4+1+2=7，
∴BC=
，
∴cosB=
=
=
AD=
=
，
故答案为：
．
可得
cosA=
| AB2+AC2-BC2 |
| 2×AB×AC |
| AB2+AD2-BD2 |
| 2×AB×BD |
BC2=AB2+AC2-2AB•ACcosA=4+1+2=7，
∴BC=
| 7 |
∴cosB=
| AB2+BC2-AC2 |
| 2×AB×BC |
| 4+7-1 | ||
2×2×
|
| 5 | ||
2
|
AD=
| AB2+BD2-2AB•BDcosB |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：本题主要考查余弦定理的应用．三角函数的综合题是高考热点，要给予重视．
练习册系列答案
同步练习河南大学出版社系列答案
同步练习西南大学出版社系列答案
补充习题江苏系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知函数f（x）=
sin（ωx+φ+
）对任意的实数x，有f（-x）=f（x），则tanφ的值为（ ）
| 2 |
| π |
| 4 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
已知α，β是两个不同的平面，m，n是直线，下列命题中不正确的是（ ）
| A、若m⊥α，n⊥α，则m∥n |
| B、若m∥α，n∥α，则m∥n |
| C、若m⊥α，m⊥β，则α∥β |
| D、若m⊥α，m?β，则α⊥β |