题目内容
已知函数f(x)=2x2+2mx+3m+4.
(1)m为何值时,f(x)有两个零点且均比-1大.
(2)求f(x)在[0,2]上的最大值g(m)
(1)m为何值时,f(x)有两个零点且均比-1大.
(2)求f(x)在[0,2]上的最大值g(m)
考点:二次函数的性质,一元二次方程的根的分布与系数的关系
专题:函数的性质及应用
分析:(1)由题意可得
,由此求得m的范围.
(2)二次函数f(x)的图象的对称轴为x=-
,再分对称轴在区间中点的左侧、右侧两种情况,结合二次函数的图象性质求得f(x)在[0,2]上的最大值g(m).
|
(2)二次函数f(x)的图象的对称轴为x=-
| m |
| 2 |
解答:
解:(1)由
,求得-6<m<3-
.
(2)二次函数f(x)的图象的对称轴为x=-
,当-
≤1时,即m≥-2时,函数f(x)在[0,2]上的最大值为g(m)=f(2)=7m+12;
当-
>1时,即m<-2时,函数f(x)在[0,2]上的最大值为g(m)=f(0)=3m+4.
|
| 17 |
(2)二次函数f(x)的图象的对称轴为x=-
| m |
| 2 |
| m |
| 2 |
当-
| m |
| 2 |
点评:本题主要考查二次函数的性质的应用,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
已知函数f(x)=
sin(ωx+φ+
)对任意的实数x,有f(-x)=f(x),则tanφ的值为( )
| 2 |
| π |
| 4 |
| A、1 | ||
| B、-1 | ||
C、
| ||
D、-
|
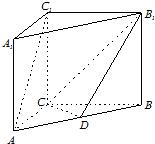 如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,AC=BC=CC1,AC⊥BC,点D是AB的中点.