题目内容
设f（x）=-3x2+（6-a）ax+b，若a=1，使f（x）＜0恒成立，求b的取值范围．
考点：二次函数的性质
专题：函数的性质及应用
分析：b＜3x2-5x，恒成立，利用函数求解y=3x2-5x的最小值，即可．
解答：
解：∵f（x）=-3x2+（6-a）ax+b，
a=1，f（x）=-3x2+5x+b，
∵f（x）＜0恒成立，
∴-3x2+5x+b＜0，
即b＜3x2-5x，恒成立，
y=3x2-5x，x=
时，最小值为-
，
即b＜-
．
a=1，f（x）=-3x2+5x+b，
∵f（x）＜0恒成立，
∴-3x2+5x+b＜0，
即b＜3x2-5x，恒成立，
y=3x2-5x，x=
| 5 |
| 6 |
| 25 |
| 12 |
即b＜-
| 25 |
| 12 |
点评：本题考查了不等式的恒成立问题，利用函数最值求解，难度不大，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图，圆O是△ABC的外接圆，∠BAC的平分线交BC于点F，D是AF的延长线与⊙O的交点，AC的延线与⊙O的切线DE交于点E．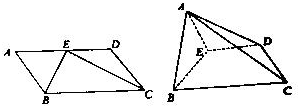
已知：平行四边形ABCD，AB=1，BC=2，∠BAD=60°，E为AD中点．将?ABCD沿BE折成直二面角．