题目内容
已知x>0,y>0,
+
=2,求2x+y的最小值.
| 1 |
| x |
| 2 |
| y+1 |
考点:基本不等式
专题:不等式的解法及应用
分析:使用基本不等式求出其最小值.
解答:
解:∵
+
=2,
∴
=2-
=
,
∴x=
∴2x+y=
+y=1+y+
≥1+2=3,当且仅当x=y=1,取等号.
故2x+y的最小值是3.
| 1 |
| x |
| 2 |
| y+1 |
∴
| 1 |
| x |
| 2 |
| y+1 |
| 2y |
| y+1 |
∴x=
| y+1 |
| 2y |
∴2x+y=
| y+1 |
| y |
| 1 |
| y |
故2x+y的最小值是3.
点评:本题考查基本不等式的应用,注意检验等号成立的条件,式子的变形是解题的关键.

练习册系列答案
相关题目
正三棱锥底面边长为3,侧棱与底面成60°角,则正三棱锥外接球面积为( )
| A、4π | ||
B、4
| ||
| C、16π | ||
D、16
|
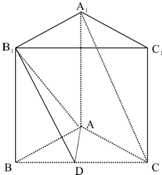 如图,正三棱柱ABC-A1B1C1中,D是BC中点,AA1=AB=a.
如图,正三棱柱ABC-A1B1C1中,D是BC中点,AA1=AB=a.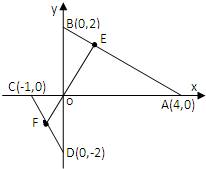 在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.
在直角坐标系中,已知A(4,0),B(0,2),C(0,-2),点E在线段AB(不含端点)上,点F在线段CD上,E、O、F三点共线.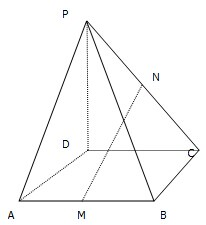 如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.
如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.