题目内容
已知命题p：2x2-9x+a＜0，命题q：
，且非q是非p的必要条件，求实数a的取值范围．
|
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：求出命题q的等价条件，利用充分条件和必要条件的定义建立条件关系即可得到结论．
解答：
解：由
，得
，解得2＜x＜3，即q：2＜x＜3，设B={x|2＜x＜3}
设A={x|2x2-9x+a＜0}，
若非q是非p的必要条件，
则p是q的必要条件，即B?A，
即当2＜x＜3时，不等式2x2-9x+a＜0恒成立，
设f（x）=2x2-9x+a，
则
，即
，
即
，解得a≤9，
故所求实数a的取值范围是{a|a≤9}
|
|
设A={x|2x2-9x+a＜0}，
若非q是非p的必要条件，
则p是q的必要条件，即B?A，
即当2＜x＜3时，不等式2x2-9x+a＜0恒成立，
设f（x）=2x2-9x+a，
则
|
|
即
|
故所求实数a的取值范围是{a|a≤9}
点评：本题主要考查充分条件和必要条件的应用，根据复合命题之间的关系以及不等式的性质，结合二次函数根的分布时解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
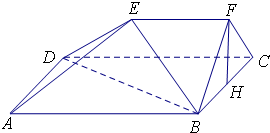如图，在五面体ABCDEF中，四边形ABCD是边长为2的正方形，EF∥平面ABCD，EF=1，FB=FC，∠BFC=90°，AE=