题目内容
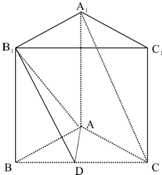 如图,正三棱柱ABC-A1B1C1中,D是BC中点,AA1=AB=a.
如图,正三棱柱ABC-A1B1C1中,D是BC中点,AA1=AB=a.(Ⅰ)求证:AD⊥B1D;
(Ⅱ)求二面角B1-AD-B余弦值的大小;
(Ⅲ)求三棱锥C-AB1D的体积.
考点:与二面角有关的立体几何综合题,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明BB1⊥AD,BC⊥AD,可得AD⊥面BB1D,即可证明AD⊥B1D;
(Ⅱ)证明∠BDB1二面角B1-AD-B的平面角,从而可求二面角B1-AD-B余弦值的大小;
(Ⅲ)利用VC-AB1D=VB1ADC,即可求三棱锥C-AB1D的体积.
(Ⅱ)证明∠BDB1二面角B1-AD-B的平面角,从而可求二面角B1-AD-B余弦值的大小;
(Ⅲ)利用VC-AB1D=VB1ADC,即可求三棱锥C-AB1D的体积.
解答:
(Ⅰ)证明:∵三棱柱ABC-A1B1C1正三棱柱,D是BC中点
∴BB1⊥AD,BC⊥AD
∵BB1∩BC=B,
∴AD⊥面BB1D,
∴AD⊥B1D
(Ⅱ)解:由(Ⅰ)知AD⊥面BB1D
∴AD⊥B1D,BC⊥AD,
∴∠BDB1二面角B1-AD-B的平面角
在RT△BB1D中BB1=a,BD=
a,
∴cos∠BDB1=
(Ⅲ)解:由图知VC-AB1D=VB1ADC,AA1=AB=a
∴VC-AB1D=VB1ADC=
S△ADCBB1=
a3.
∴BB1⊥AD,BC⊥AD
∵BB1∩BC=B,
∴AD⊥面BB1D,
∴AD⊥B1D
(Ⅱ)解:由(Ⅰ)知AD⊥面BB1D
∴AD⊥B1D,BC⊥AD,
∴∠BDB1二面角B1-AD-B的平面角
在RT△BB1D中BB1=a,BD=
| 1 |
| 2 |
∴cos∠BDB1=
| ||
| 5 |
(Ⅲ)解:由图知VC-AB1D=VB1ADC,AA1=AB=a
∴VC-AB1D=VB1ADC=
| 1 |
| 3 |
| ||
| 24 |
点评:本题考查直线与平面垂直的证明,考查二面角的求法,考查三棱锥体积的计算.解题时要认真审题,注意合理地化空间问题为平面问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
实数a、b、c满足a+b+c=0,abc>0,则
+
+
的值( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| A、一定是正数 |
| B、一定是负数 |
| C、可能是0 |
| D、正、负不能确定 |
双曲线
-
=1上一点P到它一个焦点的距离是8,则P到另一个焦点的距离是( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、18 | B、5 | C、2 | D、4 |
 在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,且△ABC为正三角形,点D是BC的中点,BC=BB1.
在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,且△ABC为正三角形,点D是BC的中点,BC=BB1.