题目内容
已知等差数列{an}中，a15=33，a45=153，求数列{an}的通项公式及S60=？
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：设出等差数列的首项和公差，直接由题意列式求出首项和公差，可求通项公式数列{an}的通项公式及S60．
解答：
解：设首项为a1，公差为d，则an=a1+（n-1）d
代入已知数据可得33=a1+14d，153=a1+44d，
解之可得a1=-23，d=4，
∴an=-23+4（n-1）=4n-27
∴S60=60•（-23）+
•4=5700．
代入已知数据可得33=a1+14d，153=a1+44d，
解之可得a1=-23，d=4，
∴an=-23+4（n-1）=4n-27
∴S60=60•（-23）+
| 60•59 |
| 2 |
点评：本题考查等差数列的通项公式与求和，涉及方程组的解法，属基础题．
练习册系列答案
相关题目
化简cos（α+β）cosα+sin（α+β）sinα得（ ）
| A、cosα |
| B、cosβ |
| C、cos（2α+β） |
| D、sin（2α+β） |
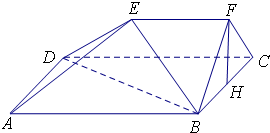如图，在五面体ABCDEF中，四边形ABCD是边长为2的正方形，EF∥平面ABCD，EF=1，FB=FC，∠BFC=90°，AE=