题目内容
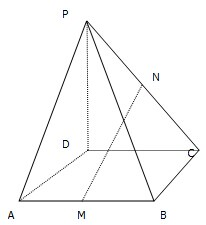 如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.
如图,在四棱锥P-ABCD中,ABCD是平行四边形,M,N分别是AB,PC的中点.1)求证:MN∥平面PAD.
2)若PD⊥AD,PD=
| 3 |
考点:直线与平面平行的判定,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:1)取CD的中点E,连接ME,NE.利用三角形中位线定理得到NE∥平面PAD.由四边形ABCD是平行四边形,得四边形AMED是平行四边形,从而得到ME∥平面PAD.由此证明平面MNE∥平面PAD,从而MN∥平面PAD.
2)由已知条件得∠EMN是异面直线MN和BC所成的角,由此能求出异面直线MN和BC所成的角.
2)由已知条件得∠EMN是异面直线MN和BC所成的角,由此能求出异面直线MN和BC所成的角.
解答:
 1)证明:取CD的中点E,连接ME,NE.
1)证明:取CD的中点E,连接ME,NE.
由N是线段CP的中点,利用三角形的中位线定理可得NE∥PD,
∵NE?平面PAD,PD?平面PAD,
∴NE∥平面PAD.
由M是线段AB的中点,E是CD的中点,四边形ABCD是平行四边形,
∴四边形AMED是平行四边形,
∴ME∥AD,可得ME∥平面PAD.
又ME∩EN=E,∴平面MNE∥平面PAD,
∴MN∥平面PAD.
2)解:∵四边形ABCD是平行四边形,四边形AMED是平行四边形,
∴ME∥BC,∴∠EMN是异面直线MN和BC所成的角,
∵PD⊥AD,PD=
,AD=1,
∴NE⊥ME,NE=
PD=
,EM=1,
∴tan∠EMN=
=
,
∴异面直线MN和BC所成的角为arctan
.
 1)证明:取CD的中点E,连接ME,NE.
1)证明:取CD的中点E,连接ME,NE.由N是线段CP的中点,利用三角形的中位线定理可得NE∥PD,
∵NE?平面PAD,PD?平面PAD,
∴NE∥平面PAD.
由M是线段AB的中点,E是CD的中点,四边形ABCD是平行四边形,
∴四边形AMED是平行四边形,
∴ME∥AD,可得ME∥平面PAD.
又ME∩EN=E,∴平面MNE∥平面PAD,
∴MN∥平面PAD.
2)解:∵四边形ABCD是平行四边形,四边形AMED是平行四边形,
∴ME∥BC,∴∠EMN是异面直线MN和BC所成的角,
∵PD⊥AD,PD=
| 3 |
∴NE⊥ME,NE=
| 1 |
| 2 |
| ||
| 2 |
∴tan∠EMN=
| NE |
| EM |
| ||
| 2 |
∴异面直线MN和BC所成的角为arctan
| ||
| 2 |
点评:本题考查直线与平面平行的证明,考查异面直线所成的角的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=
如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=