Question

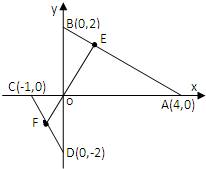在直角坐标系中，已知A（4，0），B（0，2），C（0，-2），点E在线段AB（不含端点）上，点F在线段CD上，E、O、F三点共线．
（1）若F为线段CD的中点，证明：

OE

⊥

AB

；
（2）小题（1）的逆命题是否成立？说明理由；
（3）设

AE

=λ

EB

，

DF

=μ

FC

（λ、μ∈R），求λμ的值．

Answer 1

考点：线段的定比分点,平面向量的基本定理及其意义

专题：平面向量及应用

分析：（1）由条件求得

OF

•

FB

=2-2=0，可得 OF⊥AB．再由OF∥OE可得

OE

⊥

AB

．
（2）小题（1）的逆命题成立，理由：由OF⊥AB，求得 y=2x．由C、F、D共线，可得 y=-2x-2．解方程组

y=2x y=-2x-2

，求得F的坐标，可得F为CD的中点．
（3）设E（m，n），由定比分点坐标公式可得 m、n的值．设F（x，y），由定比分点坐标公式可得x，y的值．再根据E、O、F三点共线，可得

OF

∥

OF

，xn=ym，化简可得λμ的值．

解答： 解：（1）若F为线段CD的中点，则F（-

1

2

，-1），

OF

=（-

1

2

，-1），

AB

=（-4，2），

OF

•

FB

=2-2=0，∴OF⊥AB．
又∵OF∥OE，∴

OE

⊥

AB

．
（2）小题（1）的逆命题成立，设F（x，y），由OF⊥AB 可得

OF

•

AB

=-4x+2y=0，∴y=2x．
由C、F、D共线，

CF

=（x+1，y），

CD

=（1，-2），可得

x+1

1

=

y

-2

，y=-2x-2．
解方程组

y=2x y=-2x-2

，求得

x=- 1 2 y=-1

，可得F（-

1

2

，-1），故F为CD的中点．
（3）∵

AE

=λ

EB

，设E（m，n），由定比分点坐标公式可得 m=

4+0×λ

1+λ

=

4

1+λ

，n=

0+2λ

1+λ

=

2λ

1+λ

．
∵

DF

=μ

FC

（λ、μ∈R），设F（x，y），由定比分点坐标公式可得x=

0+(-1)μ

1+μ

=

-μ

1+μ

，y=

-2+0×μ

1+μ

=

-2

1+μ

．
∵E、O、F三点共线，可得

OF

∥

OF

，∴xn=ym，
∴

-μ

1+μ

•

2λ

1+λ

=

-2

1+μ

•

4

1+λ

，化简可得λμ=4．

点评：本题主要考查平面向量基本定理、线段的定比分点坐标公式，属于基础题．