题目内容
正三棱锥底面边长为3，侧棱与底面成60°角，则正三棱锥外接球面积为（ ）
| A、4π | ||
B、4
| ||
| C、16π | ||
D、16
|
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：由题意推出球心O到四个顶点的距离相等，利用直角三角形BOE，求出球的半径，即可求出外接球的表面积．
解答：
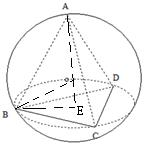解：如图，
∵正三棱锥A-BCD中，底面边长为3，
∴BE=2
，
∵侧棱与底面成60°角，
∴高AE=6
在直角三角形BOE中BO=R，EO=6-R，BE=2
，
由BO2=BE2+EO2，得R=2
∴外接球的半径为2，表面积为：16π．
故选：C．
解：如图，∵正三棱锥A-BCD中，底面边长为3，
∴BE=2
| 3 |
∵侧棱与底面成60°角，
∴高AE=6
在直角三角形BOE中BO=R，EO=6-R，BE=2
| 3 |
由BO2=BE2+EO2，得R=2
∴外接球的半径为2，表面积为：16π．
故选：C．
点评：本题是基础题，考查空间想象能力，计算能力，仔细观察和分析题意，是解好数学题目的前提．
练习册系列答案
活力课时同步练习册系列答案
相关题目
双曲线
-
=1（a＞0，b＞0）中，F为右焦点，A为左顶点，点B（0，b）且
•
=0，则此双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| BF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
实数a、b、c满足a+b+c=0，abc＞0，则
+
+
的值（ ）
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| A、一定是正数 |
| B、一定是负数 |
| C、可能是0 |
| D、正、负不能确定 |
化简cos（α+β）cosα+sin（α+β）sinα得（ ）
| A、cosα |
| B、cosβ |
| C、cos（2α+β） |
| D、sin（2α+β） |
将一个钢球置于由6根长度为
的钢管焊接成的正四面体的钢架内，那么，这个钢球的最大体积为（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
命题“平行四边形的对角线相等且互相平分”是（ ）形式命题．
| A、p∨q | B、p∧q |
| C、￢p | D、以上都不是 |
双曲线
-
=1上一点P到它一个焦点的距离是8，则P到另一个焦点的距离是（ ）
| x2 |
| 25 |
| y2 |
| 16 |
| A、18 | B、5 | C、2 | D、4 |