题目内容
7.在正项等差数列{an}中a1和a4是方程x2-10x+16=0的两个根,若数列{log2an}的前5项和为S5且S5∈[n,n+1],n∈Z,则n=11.分析 推导出an=2n,从而log2an=log2(2n)=1+log2n,进而S5=5+log21+log22+log23+log24+log25=8+log215,由此能求出结果.
解答 解:∵在正项等差数列{an}中a1和a4是方程x2-10x+16=0的两个根,
∴a1<a4,解方程得:a1=2,a4=8,d=$\frac{8-2}{4-1}$=2,
∴an=2+(n-1)×2=2n,
∴log2an=log2(2n)=1+log2n,
数列{log2an}的前5项和为S5且S5∈[n,n+1],n∈Z,
∴S5=5+log21+log22+log23+log24+log25=8+log215∈[11,12],
∴n=11.
故答案为:11.
点评 本题考查实数值的求法,考查等差数列性质,考查韦达定理、考查对数性质及运算法则,考查推理论证能力、运算求解能力,考查化归转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
17.已知圆M过定点(0,1)且圆心M在抛物线y=$\frac{1}{2}$x2上运动,若x轴截圆M所得的弦为|PQ|,则弦长|PQ|等于( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
2.函数f(x)=ax+b-1(其中0<a<1且0<b<1)的图象一定不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.三边长分别为4cm、5cm、6cm的三角形,其最大角的余弦值是( )
| A. | $-\frac{1}{8}$ | B. | $\frac{1}{8}$ | C. | $-\frac{1}{6}$ | D. | $\frac{1}{6}$ |
16.函数f(x)=sin2x-cos2x的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
14.将5本不同的书分给甲、乙、丙三人,每人至少一本至多两本,则不同的分法种数是( )
| A. | 60 | B. | 90 | C. | 120 | D. | 180 |

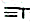 ”表示36,“
”表示36,“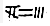 ”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )
”表示-723,函数f(x)=3xlnx-x3+83的极大值是( )