题目内容
14.将5本不同的书分给甲、乙、丙三人,每人至少一本至多两本,则不同的分法种数是( )| A. | 60 | B. | 90 | C. | 120 | D. | 180 |
分析 根据题意,分2步进行分析:①、5本不同的书分成3组,一组1本.剩余两个组每组2本,利用组合数公式可得其分组方法数目,②、将分好的三组全排列,对应甲、乙、丙三人,由排列数公式可得其情况数目,进而由分步计数原理计算可得答案.
解答 解:根据题意,分2步进行分析:
①、5本不同的书分成3组,一组1本.剩余两个组每组2本;
有$\frac{{C}_{5}^{1}{C}_{4}^{2}{C}_{2}^{2}}{{A}_{2}^{2}}$=15种分组方法;
②、将分好的三组全排列,对应甲、乙、丙三人,有A33=6种情况,
则有15×6=90种不同的分法;
故选:B.
点评 本题考查排列、组合的综合应用,涉及分步计数原理,注意先依据题意分组,进而全排列,对应三人.

练习册系列答案
 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
3.设实数a=log32,b=ln2,c=$\frac{1}{{∫}_{0}^{π}sinxdx}$,则( )
| A. | b>a>c | B. | b>c>a | C. | a>b>c | D. | a>c>b |
4.已知函数g(x)的定义域为{x|x≠0},且g(x)≠0,设p:函数$f(x)=g(x)({\frac{1}{{1-{2^x}}}-\frac{1}{2}})$是偶函数;q:函数g(x)是奇函数,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
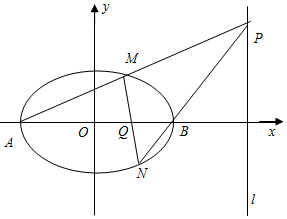 在平面直角坐标系xOy中,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左右顶点,离心率为$\frac{1}{2}$,且椭圆过定点$(1,\frac{3}{2})$,P为椭圆右准线上任意一点,直线PA,PB分别交椭圆于M,N.
在平面直角坐标系xOy中,已知A、B是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的左右顶点,离心率为$\frac{1}{2}$,且椭圆过定点$(1,\frac{3}{2})$,P为椭圆右准线上任意一点,直线PA,PB分别交椭圆于M,N.