题目内容
化简:(
)2+(
)4+(
)6+…+(
)n-1(n为奇数).
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
考点:数列的求和
专题:等差数列与等比数列
分析:当n为奇数时,(
)2+(
)4+(
)6+…+(
)n-1=(
)2+(
)4+(
)6+…+(
)2m,m∈N*,由此能求出结果.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵2=3-1,4=5-1,6=7-1,
∴n-2=2k+1-1,.即n=2k+1,k∈N*,
∴(
)2+(
)4+(
)6+…+(
)n-1(n为奇数).
=(
)2+(
)4+(
)6+…+(
)2m
=
=
(1-
),k∈N*
∴n-2=2k+1-1,.即n=2k+1,k∈N*,
∴(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
(
| ||||
1-(
|
=
| 1 |
| 3 |
| 1 |
| 4k |
点评:本题考查数列前n项和的求法,是中档题,解题时要转化认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
如图所示,AT切⊙O于T,若AT=2
,AE=3,AD=4,DE=2,则BC等于( )

| 6 |

| A、3 | B、4 | C、6 | D、8 |
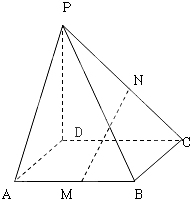 在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,M,N分别是AB,PC的中点;
在四棱锥P-ABCD中,PD⊥平面ABCD,底面是边长是1的正方形,M,N分别是AB,PC的中点;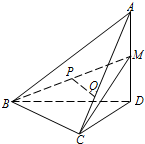 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2