题目内容
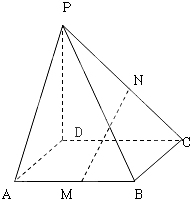在四棱锥P-ABCD中，PD⊥平面ABCD，底面是边长是1的正方形，M，N分别是AB，PC的中点；（1）求证：MN∥平面PAD；
（2）求证：BC⊥平面PCD．
考点：直线与平面垂直的判定,直线与平面平行的判定
专题：
分析：（1）做DC的中点E，连接ME，NE，通过中位线的性质证明出NE∥PD，EM∥AD，进而根据线面平行的判定定理分别证明出NE，EM平行面面ADP，进而根据面面平行的判定定理证明出面MNE∥面ADP，继而根据面面平行的性质证明出MN∥平面PAD．
（2）先分别证明出BC⊥CD，PD⊥BC，进而根据线面垂直的判定定理证明出BC⊥平面PCD．
（2）先分别证明出BC⊥CD，PD⊥BC，进而根据线面垂直的判定定理证明出BC⊥平面PCD．
解答：
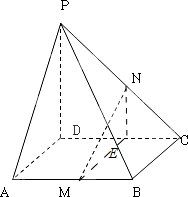证明：（1）做DC的中点E，连接ME，NE，
∵M，N，E，均为中点，
∴NE∥PD，EM∥AD，
∵PD?平面PAD，AD?平面PAD，AD∩PD=D，
∴面MNE∥面ADP，
∵MN?面MNE，
∴MN∥平面PAD．
（2）∵四边形ABCD为正方形，
∴BC⊥CD，
∵PD⊥平面ABCD，BC?平面ABCD，
∴PD⊥BC，
∵PD?平面PCD，CD?平面PCD，PD∩CD=D，
∴BC⊥平面PCD．
证明：（1）做DC的中点E，连接ME，NE，∵M，N，E，均为中点，
∴NE∥PD，EM∥AD，
∵PD?平面PAD，AD?平面PAD，AD∩PD=D，
∴面MNE∥面ADP，
∵MN?面MNE，
∴MN∥平面PAD．
（2）∵四边形ABCD为正方形，
∴BC⊥CD，
∵PD⊥平面ABCD，BC?平面ABCD，
∴PD⊥BC，
∵PD?平面PCD，CD?平面PCD，PD∩CD=D，
∴BC⊥平面PCD．
点评：本题主要考查了线面平行，线面垂直的判定定理的应用．考查了学生对线面平行，线面垂直判定定理的记忆．
练习册系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
已知各项均为正数的数列{an}满足a1=1，an+2an=39（n∈N*），那么数列{an}的前50项和S50的最小值为（ ）
| A、637 | ||
| B、559 | ||
C、481+25
| ||
D、492+24
|
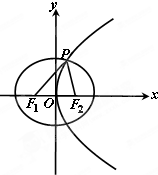已知离心率为
如图所示，四棱柱ABCD-A1B1C1D1中，底面为平行四边形，以顶点A为端点的三条棱长都为1，且两两夹角为60°，设