题目内容

由幂函数y=x
1
2
和幂函数y=x3图象围成的封闭图形面积为（　　）
A、
1
12
B、
1
4
C、
1
3
D、
5
12
考点：定积分在求面积中的应用
专题：计算题,导数的概念及应用
分析：联立两个解析式得到两曲线的交点坐标，然后对函数解析式求定积分即可得到结论．
解答： 解：两幂函数图象交点坐标是（0，0），（1，1），
所以S=
∫
1
0
(x
1
2
-x3)dx=
5
12

故选：D
点评：本题求两条曲线围成的曲边图形的面积，着重考查了定积分的几何意义和积分计算公式等知识，属于基础题．
练习册系列答案
相关题目
函数y=f（x）图象上不同两点A（x1，y1），B（x2，y2）处的切线的斜率分别是kA，kB，规定φ（A，B）=
|kA-kB|
|AB|
叫曲线y=f（x）在点A与点B之间的“弯曲度”，给出以下命题：
（1）函数y=x3-x2+1图象上两点A、B的横坐标分别为1，2，则φ（A，B）＞
3
；
（2）存在这样的函数，图象上任意两点之间的“弯曲度”为常数；
（3）设点A、B是抛物线，y=x2+1上不同的两点，则φ（A，B）≤2；
（4）设曲线y=ex上不同两点A（x1，y1），B（x2，y2），且x1-x2=1，若t•φ（A，B）＜1恒成立，则实数t的取值范围是（-∞，1）；
以上正确命题的序号为
 
（写出所有正确的）
解不等式：sinx≤-
1
2
．
函数f（x）=2cosx（x∈[-π，π]）的图象大致为（　　）
A、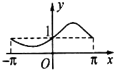
B、
C、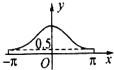
D、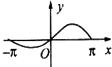
一个四面体的顶点都在球面上，它们的正视图、侧视图、俯视图都是右图．图中圆内有一个以圆心为中心边长为1的正方形．则这个四面体的外接球的表面积是（　　）
A、πB、3πC、4πD、6π
已知：四棱锥S-ABCD的底面是边长为2的正方形，点S，A，B，C，D均在半径为
3
的同一半球面上，则当四棱锥S-ABCD的体积最大时，底面ABCD的中心与顶点S之间的距离是
 
．
设函数f（x）=
1
2
cos（ωx+ϕ）对任意的x∈R，都有f（
π
6
-x）=f（
π
6
+x），若函数g（x）=3sin（ωx+ϕ）-2，则g（
π
6
）的值是（　　）
A、1
B、-5或3
C、-2
D、
1
2
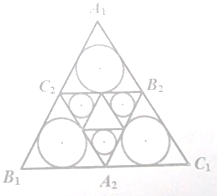设正三角形A1B1C1边长为a，分别取B1C1，C1A1，A1B1的中点A2，B2，C2，记a1是正三角形A1B1C1除去△A2B2C2后剩下的三个内切圆面积之和，依此类推：记an是△AnBnCn除去△An+1Bn+1Cn+1后剩下的三个三角形内切圆面积之和，从而得到数列{an}，设这个数列{an}的前n项和Sn．
（1）求an 和a1；
（2）求Sn，并证明Sn＜
πα2
12
．
已知函数f（x）=2
3
sinxcosx+2cos2x-1
（Ⅰ）求函数f（x）的最小正周期和函数f（x）的单调区间．
（Ⅱ）在△ABC中，角A，B，C所对的边分别是a，b，c，若f（A）=1，sinB=2sin（π-C）△ABC的面积为2
3
，求边长a的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网