题目内容

已知：四棱锥S-ABCD的底面是边长为2的正方形，点S，A，B，C，D均在半径为
3
的同一半球面上，则当四棱锥S-ABCD的体积最大时，底面ABCD的中心与顶点S之间的距离是
 
．
考点：球内接多面体
专题：计算题,空间位置关系与距离
分析：求出球心到平面的距离，然后判断底面ABCD的中心与顶点S之间的距离即可．
解答： 解：四棱锥S-ABCD的底面是边长为2的正方形，点S，A，B，C，D均在半径为
3
的同一半球面上，则当四棱锥S-ABCD的体积最大时，顶点S与底面ABCD的中心的连线经过球的中心，此时四棱锥是正四棱锥，底面中心与顶点S之间的距离，就是球的半径和球心与底面中心连线的长度之差．
球心到底面中心的距离为：
3-2
=1．
所求距离为：
3
-1．
故答案为：
3
-1．
点评：本题考查球的内接体，几何体的高的求法，考查空间想象能力以及计算能力．
练习册系列答案
相关题目
设双曲线
y2
a2
-
x2
3
=1的两个焦点分别为F1、F2，离心率为2．
（Ⅰ）求此双曲线的渐近线l1、l2的方程；
（Ⅱ）若A、B分别为l1、l2上的点，且2|AB|=5|F1F2|，求线段AB的中点M的轨迹方程，并说明轨迹是什么曲线；
（Ⅲ）过点N（1，0）能否作出直线l，使l与双曲线交于P、Q两点，且
OP
•
OQ
=0．若存在，求出直线l的方程；若不存在，说明理由．
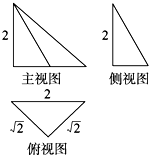
一个几何体的三视图如图所示，则该几何体的外接球的表面积为（　　）
A、36π
B、8π
C、
9
2
π
D、
27
8
π
已知平面上的曲线C及点P，在C上任取一点Q，定义线段PQ长度的最小值为点P到曲线C的距离，记作d（P，C）．若曲线C1表示直线x=-
1
2
，曲线C2表示射线y=0（x≥
1
2
），则点集{P|d（P，C1）=d（P，C2）}所表示的图形是（　　）
A、
B、
C、
D、
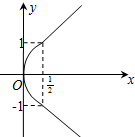
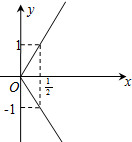
由幂函数y=x
1
2
和幂函数y=x3图象围成的封闭图形面积为（　　）
A、
1
12
B、
1
4
C、
1
3
D、
5
12
在区间[1，5]上任取一个数m，则函数y=x2-4x-2（0≤x≤m）的值域为[-6，-2]的概率是
 
．
某同学用“五点法”画函数f（x）=Asin（ωx+ϕ）+k（A＞0，ω＞0，|ϕ|＜
π
2
）在一个周期内的图象，列表并填入数据得到下表：
xx1
π
6
x2
2π
3
x3
ωx+ϕ0
π
2
π
3π
2
2π
f（x）y13y2-1y3
（1）求函数f（x）的解析式；
（2）三角形ABC中，角A，B，C所对的边分别是a，b，c，若f（B）=2，b=4，acos2
C
2
+ccos2
A
2
=6，求三角形ABC的面积．
已知A（3，5），B（6，9），且|
AM
|=3|
MB
|，M是直线AB上一点，求点M的坐标．
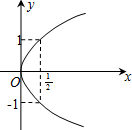
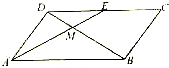如图，在平行四边形ABCD中，E为DC的中点，AE与BD交于点E，AB=
2
，AD=1，且
MA
•
MB
=-
1
6
，则
AB
•
AD
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网