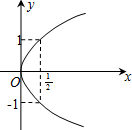题目内容
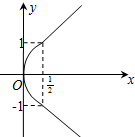
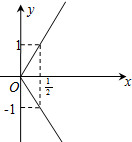
函数f(x)=2cosx(x∈[-π,π])的图象大致为( )
A、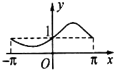 |
B、 |
C、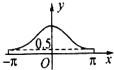 |
D、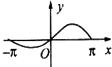 |
考点:函数的图象
专题:函数的性质及应用
分析:由f(-x)=2cos(-x)=2cosx=f(x),得出f(x)为偶函数,则图象关于y轴对称,排除A、D,再令x=π代入f(x)的表达式即可得到答案.
解答:
解:∵f(-x)=2cos(-x)=2cosx=f(x),∴f(x)为偶函数,则图象关于y轴对称,排除A、D,
把x=π代入得f(π)=20=1,故图象过点(π,1),B选项适合,
故选:B.
把x=π代入得f(π)=20=1,故图象过点(π,1),B选项适合,
故选:B.
点评:本题主要考查学生的识图能力,由函数所满足的性质排除一些选项,再结合特殊值,易得答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=x2+1的图象在点A(x1,f(x1))与点B(x2,f(x2))处的切线互相垂直,并交于点P,则点P的坐标可能是( )
A、(
| ||
B、(0,
| ||
| C、(1,3) | ||
D、(1,
|
一个几何体的三视图如图所示,则该几何体的外接球的表面积为( )
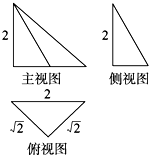

| A、36π | ||
| B、8π | ||
C、
| ||
D、
|
由幂函数y=x
和幂函数y=x3图象围成的封闭图形面积为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|