题目内容
已知集合A={x|x2-3x-10<0},B={x|m+1≤x≤2m-1}.
(1)当m=3时,求集合A∩B(∁RA)∩B;
(2)若A∩B=B,求实数m的取值范围.
(1)当m=3时,求集合A∩B(∁RA)∩B;
(2)若A∩B=B,求实数m的取值范围.
考点:交、并、补集的混合运算
专题:集合
分析:(1)求出A中不等式的解集确定出A,把m的值代入B确定出B,求出A与B的交集,找出A补集与B的交集即可;
(2)由题意得到B为A的子集,分B为空集与不为空集两种情况求出m的范围即可.
(2)由题意得到B为A的子集,分B为空集与不为空集两种情况求出m的范围即可.
解答:
解:(1)由A中不等式解得:-2<x<5,即A={x|-2<x<5},
当m=3时,B中不等式为4≤x≤5,即B={x|4≤x≤5},
∴A∩B={x|4≤x<5},∁RA={x|x≤-2或x≥5},
则(∁RA)∩B={5};
(2)∵A∩B=B,∴B⊆A,
①当B=∅时,m+1>2m-1,即m<2,此时B⊆A;
②当B≠∅时,
,即2≤m<3,此时B⊆A,
综上所述,m的取值范围是{m|2≤m<3}.
当m=3时,B中不等式为4≤x≤5,即B={x|4≤x≤5},
∴A∩B={x|4≤x<5},∁RA={x|x≤-2或x≥5},
则(∁RA)∩B={5};
(2)∵A∩B=B,∴B⊆A,
①当B=∅时,m+1>2m-1,即m<2,此时B⊆A;
②当B≠∅时,
|
综上所述,m的取值范围是{m|2≤m<3}.
点评:此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数y=x2-4x+7的值域是( )
| A、{y|y∈R} |
| B、{y|y≥3} |
| C、{y|y≥7} |
| D、{y|y>3} |
若复数z满足iz=1+2i,则在复平面内,z的共轭复数
对应的点所在象限是( )
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
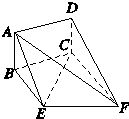 如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=
如图,矩形ABCD和梯形BEFC所在平面互相垂直,∠BCF=∠CEF=90°,AD=